Q. No.A particle moving in a straight line covers half the distance with a speed of \(3~\text{m/s}\). The other half of the distance is covered in two equal time intervals with speeds of \(4.5~\text{m/s}\) and \(7.5~\text{m/s}\) respectively. The average speed of the particle during this motion is:
1.
\(4.0~\text{m/s}\)
2.
\(5.0~\text{m/s}\)
3.
\(5.5~\text{m/s}\)
4.
\(4.8~\text{m/s}\)
A particle starts from rest. Its acceleration \((a)\) versus time \((t)\) is as shown in the figure. The maximum speed of the particle will be:
1. \(110~\text{m/s}\)
2. \(55~\text{m/s}\)
3. \(550~\text{m/s}\)
4. \(660~\text{m/s}\)
A stone dropped from a building of height \(h\) and reaches the earth after \(t\) seconds. From the same building, if two stones are thrown (one upwards and other downwards) with the same velocity \(u\) and they reach the earth surface after \(t_1\) and \(t_2\) seconds respectively, then:
1.
2.
3.
4.
A particle is dropped vertically from rest from a height. The time taken by it to fall through successive distances of \(1~\text{m}\) each will then be:
| 1. | All equal, being equal to \(\sqrt{2 / g} \) s. |
| 2. | In the ratio of the square roots of the integers \(1,2,3....\) |
| 3. | In the ratio of the difference in the square roots of the integers \(\sqrt{1}\), \((\sqrt{2}-\sqrt{1})\),\((\sqrt{3}-\sqrt{2})\),\((\sqrt{4}-\sqrt{3})\) \( \ldots\) |
| 4. | In the ratio of the reciprocal of the square roots of the integers i.e,... \(\frac{1}{\sqrt{1}}\), \(\frac{1}{\sqrt{2}}\), \(\frac{1}{\sqrt{3}}\),\(\frac{1}{\sqrt{4}} \) |
The graph between the displacement \(x\) and time \(t\) for a particle moving in a straight line is shown in the figure.
During the interval OA, AB, BC and CD the acceleration of the particle is:
| OA | AB | BC | CD | |
| 1. | + | 0 | + | + |
| 2. | – | 0 | + | 0 |
| 3. | + | 0 | – | + |
| 4. | – | 0 | – | 0 |
A lift is going up. The variation in the speed of the lift is as given in the graph. What is the height to which the lift takes the passengers?
| 1. | \(3.6~\text{m}\) |
| 2. | \(28.8~\text{m}\) |
| 3. | \(36.0~\text{m}\) |
| 4. | It cannot be calculated from the above graph. |
The velocity-time \((v\text-t)\) graph of a body moving in a straight line is shown in the figure. The displacement and distance travelled by the body in \(6\) s are, respectively:
1. \(8\) m, \(16\) m
2. \(16\) m, \(8\) m
3. \(16\) m, \(16\) m
4. \(8\) m, \(8\) m
In the following graph, the distance travelled by the body in metres is:
| 1. | \(200\) | 2. | \(250\) |
| 3. | \(300\) | 4. | \(400\) |
Which of the following velocity-time graphs shows a realistic situation for a body in motion?
| 1. |  |
2. |  |
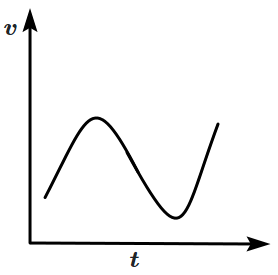| 3. |  |
4. |  |
© 2024 GoodEd Technologies Pvt. Ltd.