The position of an object moving along the \(x\text-\)axis is given by, \(x=a+bt^2\), where \(a=8.5 ~\text m,\) \(b=2.5~\text{m/s}^2,\) and \(t\) is measured in seconds. Its velocity at \(t=2.0~\text s\) will be:
1. \(13~\text{m/s}\)
2. \(17~\text{m/s}\)
3. \(10~\text{m/s}\)
4. \(0~\text{m/s}\)
1. \(13~\text{m/s}\)
2. \(17~\text{m/s}\)
3. \(10~\text{m/s}\)
4. \(0~\text{m/s}\)
The position-time graph for a free-falling object is:
| 1. | a parabolic curve | 2. | a straight line |
| 3. | a circular curve | 4. | an elliptical curve |
A train is moving in the north direction with a speed of \(54\) . The velocity of a monkey running on the roof of the train against its motion (with a velocity of \(18\) with respect to the train) as observed by a man standing on the ground is:
1. \(40\) ms-1
2. \(0\)
3. \(-5\) ms-1
4. \(10\) ms-1
Two parallel rail tracks run north-south. Train A moves north with a speed of 54 , and train B moves south with a speed of 90 . The magnitude of the velocity of B with respect to A is:
1. 40
2. 0
3. 25
4. 15
A train is moving in south with a speed of 90 . The velocity of ground with respect to the train is:
1. 0
2. -25
3. 25
4. -40
Galileo’s law of odd numbers: The distances traversed, during equal intervals of time, by a body falling from rest, stand to one another in the ratio:
| 1. | as the odd numbers beginning with unity. |
| 2. | as the even numbers beginning with unity. |
| 3. | as the square of odd numbers beginning with unity. |
| 4. | as the square of even numbers beginning with unity. |
You can measure your reaction time by a simple experiment. Take a ruler and ask your friend to drop it vertically through the gap between your thumb and forefinger (figure shown below). After you catch it if the distance d travelled by the ruler is \(21.0\) cm, your reaction time is:
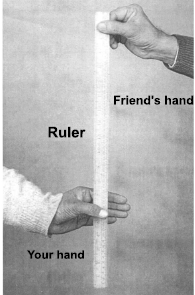
| 1. | \(0.2\) s | 2. | \(0.4\) s |
| 3. | \(0\) | 4. | \(0.1\) s |
When brakes are applied to a moving vehicle, the distance it travels before stopping is called stopping distance. It is an important factor for road safety and depends on the initial velocity \({v_0}\) and the braking capacity, or deceleration, \(-a\) that is caused by the braking. Expression for stopping distance of a vehicle in terms of \({v_0}\) and \(a\) is:
| 1. | \(\dfrac{{v_o}^2}{2a}\) | 2. | \(\dfrac{{v_o}}{2a}\) |
| 3. | \(\dfrac{{v_o}^2}{a}\) | 4. | \(\dfrac{2a}{{v_o}^2}\) |
A ball is thrown vertically upwards with a velocity of \(20\) m/s from the top of a multistorey building. The height of the point from where the ball is thrown is \(25.0\) m from the ground. How long will it be before the ball hits the ground?
(Take \(g=10\) ms–2.)
1. \(3\) s
2. \(2\) s
3. \(5\) s
4. \(20\) s
(Take \(g=10\) m/s2)
| 1. | \(30\) m | 2. | \(25\) m |
| 3. | \(45\) m | 4. | \(20\) m |






