If \(a,b,c,\) and \(d\) are inputs to a logic gate and \(x\) is its output, then based on the timing diagram shown below, what type of gate is this?
| 1. | NOT | 2. | AND |
| 3. | OR | 4. | NAND |
The logic gate equivalent to the given logic circuit is:
1. AND
2. OR
3. NOR
4. NAND
The truth table for the circuit given in the fig. is:
| 1. | \(A\) | \(B\) | \(Y\) | 2. | \(A\) | \(B\) | \(Y\) |
| 0 | 0 | 1 | 0 | 0 | 1 | ||
| 0 | 1 | 1 | 0 | 1 | 1 | ||
| 1 | 0 | 1 | 1 | 0 | 0 | ||
| 1 | 1 | 1 | 1 | 1 | 0 | ||
| 3. | \(A\) | \(B\) | \(Y\) | 4. | \(A\) | \(B\) | \(Y\) |
| 0 | 0 | 0 | 0 | 0 | 1 | ||
| 0 | 1 | 0 | 0 | 1 | 0 | ||
| 1 | 0 | 1 | 1 | 0 | 0 | ||
| 1 | 1 | 1 | 1 | 1 | 0 | ||
In the digital logic circuit shown, what is the sequence of output values at terminal \(Z\) corresponding to the input combinations \((A,B)=(1,0),(0,0),(1,1)\) and \((0,1)\text{?}\)
| 1. | \(1,0,1,1\) |
| 2. | \(0,1,0,0\) |
| 3. | \(0,0,1,0\) |
| 4. | \(1,1,0,1\) |
Identify the operation performed by the circuit given below:
1. \(\text{OR}\)
2. \(\text{NOT}\)
3. \(\text{NAND}\)
4. \(\text{AND}\)
The logic circuit shown above is equivalent to :
| 1. | 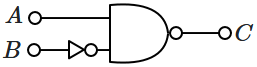 |
| 2. |  |
| 3. |  |
| 4. |  |
The truth table for the following logic circuit is :
| 1. | A | B | Y | 2. | A | B | Y | |
| 0 | 0 | 0 | 0 | 0 | 1 | |||
| 0 | 1 | 1 | 0 | 1 | 0 | |||
| 1 | 0 | 1 | 1 | 0 | 0 | |||
| 1 | 1 | 0 | 1 | 1 | 1 | |||
| 3. | A | B | Y | 4. | A | B | Y | |
| 0 | 0 | 1 | 0 | 0 | 0 | |||
| 0 | 1 | 0 | 0 | 1 | 1 | |||
| 1 | 0 | 1 | 1 | 0 | 0 | |||
| 1 | 1 | 0 | 1 | 1 | 1 | |||
Draw the output signal \(Y\) in the given combination of gates :
| 1. |  |
| 2. |  |
| 3. |  |
| 4. |  |

1. AND gate
2. OR gate
3. NOR gate
4. NAND gate

| 1. |  |
| 2. |  |
| 3. |  |
| 4. | none of these |














