The modulus of rigidity of the ideal liquid is:
1. infinity
2. zero
3. unity
4. some finite small non-zero constant value
| (a) | The bulk modulus is infinite. |
| (b) | The bulk modulus is zero. |
| (c) | The shear modulus is infinite. |
| (d) | The shear modulus is zero. |
Choose the correct option from the options given below:
| 1. | (a) and (d) only |
| 2. | (b) and (d) only |
| 3. | (b) and (c) only |
| 4. | (c) and (d) only |
| (a) | the same stress | (b) | different stress |
| (c) | the same strain | (d) | different strain |
Choose the correct option:
| 1. | (a), (b) | 2. | (a), (d) |
| 3. | (b), (c) | 4. | (c), (d) |
On withdrawing the external applied force on bodies within the elastic limit, the body:
| 1. | regains its previous state very quickly |
| 2. | regains its previous state after some time |
| 3. | regains its previous state after a very long time |
| 4. | does not regain its previous state |
If two different types of rubber are found to have stress-strain curves as shown, then:
| 1. | A is suitable for shock absorbers. |
| 2. | B is suitable for shock absorbers. |
| 3. | B is suitable for car tires. |
| 4. | None of these |
The figure shows the graph between stress and strain for a uniform wire at two different temperatures. Then:
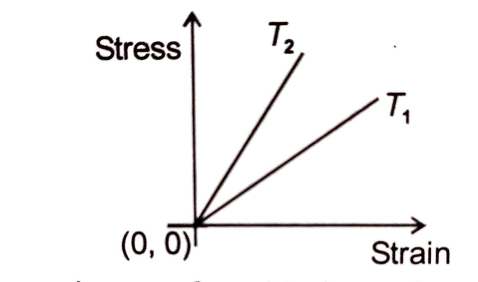
1. \(T_1>T_2\)
2. \(T_2>T_1\)
3. \(T_1=T_2\)
4. None of these
Hooke's law is applicable for:
| 1. | elastic materials only | 2. | plastic materials only |
| 3. | elastomers only | 4. | all of these |

| 1. | \(0.7\) m from wire \(A\) |
| 2. | \(0.07\) m from wire \(A\) |
| 3. | \(7.0\) m from wire \(A\) |
| 4. | \(0.007\) m from wire \(A\) |
Anvils made of single crystals of diamond, with the shape as shown in the figure, are used to investigate the behaviour of materials under very high pressures. Flat faces at the narrow end of the anvil have a diameter of \(0.50\) mm, and the wide ends are subjected to a compressional force of \(50,000\) N. What is the pressure at the tip of the anvil?
1. \(2.5\times10^{11}\) Pa
2. \(3.7\times10^{11}\) Pa
3. \(2.1\times10^{11}\) Pa
4. \(1.9\times10^{11}\) Pa
The volume contraction of a solid copper cube, \(10~\text{cm}\) on an edge, when subjected to a hydraulic pressure of \(7.0\times10^6~\text{Pa}\) is:
(Bulk modulus of copper is \(140 \times10^{9}~\text{Pa}.\))
1. \( 3.1 \times 10^{-2} ~\text{m}^3 \)
2. \(9.1 \times 10^{-3} ~\text{cm}^3 \)
3. \(5.0 \times 10^{-2} ~\text{cm}^3 \)
4. \(7.9 \times 10^{-2} ~\text{cm}^3 \)




