- 1(current)
Q. No.Given below are two statements:
| Assertion (A): | The graph between velocity and displacement for a simple harmonic motion is an ellipse. |
| Reason (R): | Velocity does not change uniformly with displacement in simple harmonic motion. |
| 1. | Both (A) and (R) are True and (R) is the correct explanation of (A). |
| 2. | Both (A) and (R) are True but (R) is not the correct explanation of (A). |
| 3. | (A) is True but (R) is False. |
| 4. | Both (A) and (R) are False. |
Subtopic: Â Simple Harmonic Motion |
From NCERT
To view explanation, please take trial in the course.
NEET 2026 - Target Batch
Hints
To view explanation, please take trial in the course.
NEET 2026 - Target Batch
Given below are two statements:
| Assertion (A): | Acceleration of a particle in SHM is always zero. |
| Reason (R): | Two SHMs must have the same phase if the amplitude is same. |
| 1. | Both (A) and (R) are true and (R) is the correct explanation of (A). |
| 2. | Both (A) and (R) are true but (R) is not the correct explanation of (A). |
| 3. | (A) is true but (R) is false. |
| 4. | Both (A) and (R) are false. |
Subtopic: Â Simple Harmonic Motion |
 84%
From NCERT
To view explanation, please take trial in the course.
NEET 2026 - Target Batch
Hints
To view explanation, please take trial in the course.
NEET 2026 - Target Batch
Given below are two statements:
| Assertion (A): | In simple harmonic motion, the motion is to and fro and periodic. |
| Reason (R): | In simple harmonic motion, the particle's velocity is given by \(v=\omega \sqrt {A^2-x^2},\) (where \(x\) is the displacement of the particle). |
| 1. | Both (A) and (R) are True and (R) is the correct explanation of (A). |
| 2. | Both (A) and (R) are True but (R) is not the correct explanation of (A). |
| 3. | (A) is True but (R) is False. |
| 4. | Both (A) and (R) are False. |
Subtopic: Â Simple Harmonic Motion |
 85%
From NCERT
To view explanation, please take trial in the course.
NEET 2026 - Target Batch
Hints
To view explanation, please take trial in the course.
NEET 2026 - Target Batch
The (displacement-time) graph of a particle executing SHM is shown in the figure. Then:
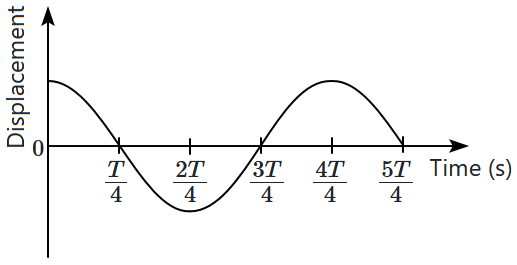
| (a) | the force is zero at \(t=\dfrac{3T}{4}\) |
| (b) | the acceleration is maximum at \(t=\dfrac{4T}{4}\) |
| (c) | the velocity is maximum at \(t=\dfrac{T}{4}\) |
| (d) | the potential energy is equal to the kinetic energy of oscillation at \(t=\dfrac{T}{2}\) |
| 1. | (a), (b) and (d) only | 2. | (a), (b) and (c) only |
| 3. | (b), (c) and (d) only | 4. | (c) and (d) only |
Subtopic: Â Simple Harmonic Motion |
 68%
From NCERT
To view explanation, please take trial in the course.
NEET 2026 - Target Batch
Hints
To view explanation, please take trial in the course.
NEET 2026 - Target Batch
The velocity-time diagram of a harmonic oscillator is shown in the figure given below. The frequency of oscillation will be:
1. \(25~\text{Hz}\)
2. \(50~\text{Hz}\)
3. \(12.25~\text{Hz}\)
4. \(33.3~\text{Hz}\)
Subtopic: Â Simple Harmonic Motion |
 75%
From NCERT
To view explanation, please take trial in the course.
NEET 2026 - Target Batch
Hints
To view explanation, please take trial in the course.
NEET 2026 - Target Batch
The variation of acceleration, \(a\) of a particle executing SHM with displacement \(x\) is:
| 1. |  |
2. |  |
| 3. |  |
4. |  |
Subtopic: Â Simple Harmonic Motion |
 69%
From NCERT
To view explanation, please take trial in the course.
NEET 2026 - Target Batch
Hints
To view explanation, please take trial in the course.
NEET 2026 - Target Batch
- 1(current)
Q. No.
© 2025 GoodEd Technologies Pvt. Ltd.