Q. No.Three particles of masses \(100~\text{g}\), \(150~\text{g}\), and \(200~\text{g}\) respectively are placed at the vertices of an equilateral triangle of a side \(0.5~\text{m}\) long. What is the position of the centre of mass of three particles?
2. \(\left(\dfrac{1}{4} , 0\right) \)
3. \(\left(0 , \dfrac{1}{4}\right) \)
4. \(\left(\dfrac{1}{3 \sqrt{3}} , \dfrac{5}{18}\right) \)
Position of centre of mass of a triangular lamina as shown in the figure is:
2. at the point \(G\).
3. at the point \(L\).
4. can't be determined.
What is the position of centre of mass of a uniform L-shaped lamina (a thin flat plate) with dimensions as shown? The mass of the lamina is 3 kg.
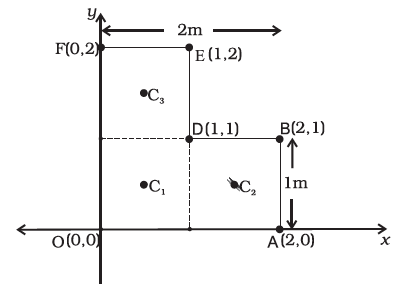
| 1. | \(\left(\dfrac{6}{5} , \dfrac{6}{5}\right)\) | 2. | \(\left(\dfrac{1}{5} , \dfrac{6}{5}\right)\) |
| 3. | \(\left(\dfrac{5}{6} , \dfrac{5}{6}\right)\) | 4. | Can't be determined |
If the force \(7\hat i+3\hat j-5\hat k\) acts on a particle whose position vector is \(\hat i - \hat j+\hat k\), the torque of the force about the origin is?
1. \(2\hat i +12\hat j+10\hat k\)
2. zero
3. \(2\hat i -12\hat j-10\hat k\)
4. \(2\hat i +12\hat j-10\hat k\)
The angular momentum about any point of a single particle moving with constant velocity:
| 1. | increases continuously. |
| 2. | decreases continuously. |
| 3. | first increases then decrease. |
| 4. | remains constant throughout the motion. |
Moment of a couple:
| 1. | depends on the point about which you take the moments |
| 2. | depends on the reference frame |
| 3. | does not depend on the point about which you take the moments |
| 4. | does not depend on the direction of the forces |
A metal bar 70 cm long and 4.00 kg in mass supported on two knife edges placed 10 cm from each end. A 6.00 kg load is suspended at 30 cm from one end as shown in the figure. The reactions at the knife-edges are: (Assume the bar to be of uniform cross-section and homogeneous.)
2. 54.88 N and 4.312 N
3. 54.88 N and 43.12 N
4. 43.12 N and 5.488 N
A \(3~\text{m}\) long ladder weighing \(20~\text{kg}\) leans on a frictionless wall. Its feet rest on the floor \(1~\text{m}\) from the wall as shown in the figure. The reaction forces of the wall and the floor respectively are:
| 1. | \(30.4~\text{N}\) and \(198~\text{N}\) |
| 2. | \(199~\text{N}\) and \(30~\text{N}\) |
| 3. | \(34.6~\text{N}\) and \(199~\text{N}\) |
| 4. | \(34.6~\text{N}\) and \(199~\text{N}\) |
The moment of inertia of a disc about one of its diameters is:
| 1. | \(MR^2\) | 2. | \(\dfrac{MR^2}{3}\) |
| 3. | \(\dfrac{2MR^2}{3}\) | 4. | \(\dfrac{MR^2}{4}\) |
The moment of inertia of a rod of mass M, length l about an axis perpendicular to it through one end is:
1.
2.
3.
4. Can't be determined
© 2024 GoodEd Technologies Pvt. Ltd.