The electrostatic force between the metal plates of an isolated parallel plate capacitor \(C\) having a charge \(Q\) and area \(A\) is:
| 1. | independent of the distance between the plates. |
| 2. | linearly proportional to the distance between the plates. |
| 3. | proportional to the square root of the distance between the plates. |
| 4. | inversely proportional to the distance between the plates. |
The diagrams below show regions of equipotentials.
| 1. | the maximum work is required to move \(q\) in figure(iii). |
| 2. | in all four cases, the work done is the same. |
| 3. | the minimum work is required to move \(q\) in the figure(i). |
| 4. | the maximum work is required to move \(q\) in figure(ii). |
A capacitor is charged by a battery. The battery is removed and another identical uncharged capacitor is connected in parallel. The total electrostatic energy of the resulting system:
| 1. | decreases by a factor of \(2\) |
| 2. | remains the same |
| 3. | increases by a factor of \(2\) |
| 4. | increases by a factor of \(4\) |
1. \(8~\text{mC}\)
2. \(2~\text{mC}\)
3. \(5~\text{mC}\)
4. \(7~\mu\text{C}\)
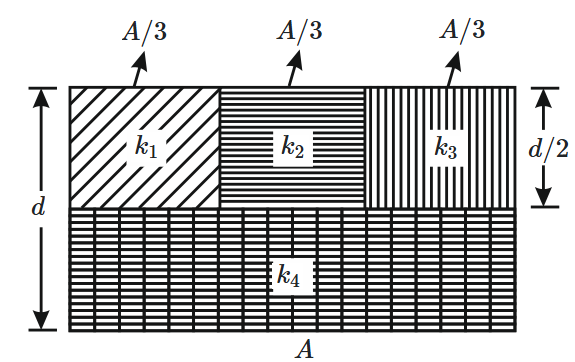
1. \(k = k_{1} + k_{2} + k_{3} + 3 k_{4}\)
3. \(\dfrac{1}{k} = \dfrac{3}{2 \left(k_{1} + k_{2} + k_{3}\right)} + \dfrac{1}{2 k_{4}}\)
4. \(\dfrac{1}{k} = \dfrac{1}{k_{1}} + \dfrac{1}{k_{2}} + \dfrac{1}{k_{3}} + \dfrac{3}{2 k_{4}}\)
A capacitor of \(2~\mu\text{F}\) is charged as shown in the figure. When the switch \({S}\) is turned to position \(2,\) the percentage of its stored energy dissipated is:
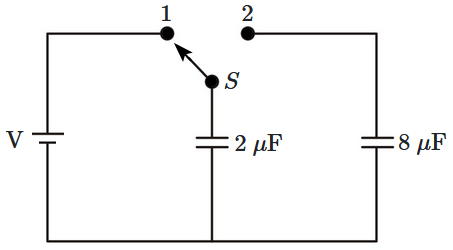
2. \(75\%\)
3. \(80\%\)
4. \(0\%\)





