The vector sum of two forces is perpendicular to their vector difference. In that case, the forces:

1.	are not equal to each other in magnitude.
2.	cannot be predicted.
3.	are equal to each other.
4.	are equal to each other in magnitude.

If the angle between the two forces increases, the magnitude of their resultant:

1. Decreases

2. Increases

3. Remains unchanged

4. First decreases, then increases

The incorrect statement/s is/are:
1. (b), (d)
2. (a), (c)
3. (b), (c), (d)
4. (a), (b)

If the sum of two unit vectors is also a unit vector, then the magnitude of their difference and angle between the two given unit vectors is:
1. \(\sqrt{3}, 60^{\circ}\)
2. \(\sqrt{3}, 120^{\circ}\)
3. \(\sqrt{2}, 60^{\circ}\)
4. \(\sqrt{2},120^{\circ}\)

Let \(\theta\) be the angle between vectors \(\overrightarrow A\) and \(\overrightarrow {B}\). Which of the following figures correctly represents the angle \(\theta\)?

1.		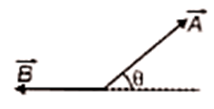2.
3.		4.

The dot product of two mutual perpendicular vector is:

1. \(0\)

2. \(1\)

3. \(\infty\)

4. None of the above

The angle between vectors $\left(\overrightarrow{\mathrm{A}}\times \overrightarrow{\mathrm{B}}\right)$ and $\left(\overrightarrow{\mathrm{B}}\times \overrightarrow{\mathrm{A}}\right)$ is:
1. zero
2. $\mathrm{\pi }$
3. $\mathrm{\pi }/4$
4. $\mathrm{\pi }/2$

If for two vectors \(\overrightarrow{A}\) and \(\overrightarrow {B}\), \(\overrightarrow {A}\times \overrightarrow {B}=0\), then the vectors:

A particle moves from position null to \(\left(11\hat i + 11\hat j + 15\hat k \right)\) due to a uniform force of \(\left(4\hat i + \hat j + 3\hat k\right)\)N. If the displacement is in m, then the work done will be: (Given: \(W=\overrightarrow {F}.\overrightarrow {S}\))
1. \(100~\text{J}\)
2. \(200~\text{J}\)
3. \(300~\text{J}\)
4. \(250~\text{J}\)

There are two force vectors, one of \(5~\text{N}\) and the other of \(12~\text{N}\). At what angle should the two vectors be added to get the resultant vector of \(17~\text{N}, 7~\text{N},\) and \(13~\text{N}\) respectively:
1. \(0^{\circ}, 180^{\circ}~\text{and}~90^{\circ}\)
2. \(0^{\circ}, 90^{\circ}~\text{and}~180^{\circ}\)
3. \(0^{\circ}, 90^{\circ}~\text{and}~90^{\circ}\)
4. \(180^{\circ}, 0^{\circ}~\text{and}~90^{\circ}\)