An electron falls through a distance of \(1.5~\text{cm}\) in a uniform electric field of magnitude \(2\times10^4~\text{N/C}\) [figure (a)]. The direction of the field is reversed keeping its magnitude unchanged and a proton falls through the same distance [figure (b)]. If \(t_e\) and \(t_p\) are the time of fall for electron and proton respectively, then:

   
1. \(t_e=t_p\)
2. \(t_e>t_p\)
3. \(t_e<t_p\)
4. none of these$\mathrm{}$

Two-point charges $q_1$ and $q_2$, of magnitude $+{10}^{-8} C$  and $-{10}^{-8} C$, respectively, are placed 0.1 m apart. The electric field at point  A (as shown in the figure) is: 

$1. 3.6\times {10}^4 {\mathrm{NC}}^{-1}$
$2. 7.2\times {10}^4 {\mathrm{NC}}^{-1}$
$3. 9\times {10}^3 {\mathrm{NC}}^{-1}$
$4. 3.2\times {10}^4 {\mathrm{NC}}^{-1}$

Two charges \(\pm10~\mu\text{C}\) are placed \(5.0\) mm apart. The electric field at a point \(P\) on the axis of the dipole \(15\) cm away from its centre \(O\) on the side of the positive charge, as shown in the figure is:

Two charges \(\pm 10~ \mu \text{C}\) are placed \(5.0\) mm apart. The electric field at a point \(Q\), \(15\) cm away from \(O\) on a line passing through \(O\) and normal to the axis of the dipole, as shown in the figure is:

$\mathrm{}$1. \(2.8 \times 10^5~\text{NC}^{-1}\)
2. \(3.9\times 10^5 ~\text{NC}^{-1}\)
3. \(1.33\times 10^5 ~\text{NC}^{-1}\)
4. \(4.1\times 10^6 ~\text{NC}^{-1}\)$\mathrm{}$

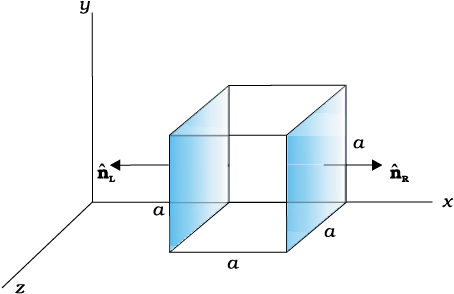
The electric field components in the shown figure are ${\mathrm{E}}_{\mathrm{x}}=\alpha x^{1/2}$, E_y = E_z = 0, in which  $\mathrm{\alpha }=800 \mathrm{N}/\mathrm{C} {\mathrm{m}}^{1/2}$. The net flux through the cube is: (Assume that a = 0.1 m)

$1. 1.05 {\mathrm{Nm}}^2{\mathrm{C}}^{-1}$
$2. 2.03 {\mathrm{Nm}}^2{\mathrm{C}}^{-1}$
$3. 3.05 {\mathrm{Nm}}^2{\mathrm{C}}^{-1}$
$4. 4.03 {\mathrm{Nm}}^2{\mathrm{C}}^{-1}$

The electric field components in the shown figure are ${\mathrm{E}}_{\mathrm{x}}={\mathrm{ax}}^{1/2}$, E_y = E_z = 0, in which  $\mathrm{\alpha }=800 \mathrm{N}/\mathrm{C} {\mathrm{m}}^{1/2}$. Find the charge within the cube if net flux through the cube is $1.05 \mathrm{N} {\mathrm{m}}^2 {\mathrm{C}}^{-1}$: (Assume that a = 0.1 m). 

$1. \mathrm{Zero}$
$2. 2.7\times {10}^{-12} \mathrm{C}$
$3. 7.9\times {10}^{-12} \mathrm{C}$
$4. 9.2\times {10}^{-12} \mathrm{C}$

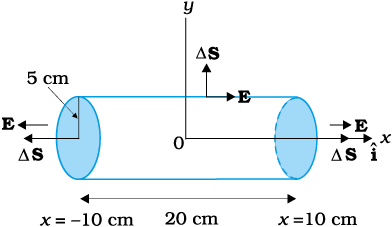
An electric field is uniform, and in the positive \(x\)-direction for positive \(x\), and uniform with the same magnitude but in the negative \(x\)-direction for negative \(x\). It is given that \(\vec{E}=200\hat{i}\) N/C for \(x>0\) and \(\vec{E}=-200\hat{i}\)  N/C for \(x<0\). A right circular cylinder of length \(20~\text{cm}\) and radius \(5~\text{cm}\) has its centre at the origin and its axis along the \(x\text{-}\)axis so that one face is at \(x= + 10~\text{cm}\) and the other is at \(x= -10~\text{cm}\) (as shown in the figure). What is the net outward flux through the cylinder?

1. \(0\)
2. \(1.57~\text{Nm}^2\text{C}^{-1}\)
3. \(3.14~\text{Nm}^2\text{C}^{-1}\)
4. \(2.47~\text{Nm}^2\text{C}^{-1}\)

An electric field is uniform, and in the positive x-direction for positive x, and uniform with the same magnitude but in the negative x-direction for negative x. It is given that E =$200 \hat{i}$ N/C for x > 0 and E = –$200 \hat{i}$ N/C for x < 0. A right circular cylinder of length 20 cm and radius 5 cm has its centre at the origin and its axis along the x-axis so that one face is at x = +10 cm and the other is along the x-axis so that one face is at x = +10 cm and the other is at x = –10 cm (as shown in the figure). What is the net charge inside the cylinder?

$1. 2.78\times {10}^{-11} C$
$2 3.10\times {10}^{-12} C$
$3. 1.37\times {10}^{-10} C$
$4. 2.62\times {10}^{-12} C$

An early model for an atom considered it to have a positively charged point nucleus of charge Ze, surrounded by a uniform density of negative charge up to a radius R. The atom as a whole is neutral. For this model, the electric field at a distance r (r>R) from the nucleus is:

$1. \frac{Ze}{4\pi {\epsilon }_0}\left(\frac{1}{r^2}-\frac{r}{R^3}\right)$
$2. 0$
$3. \frac{Ze}{4\pi {\epsilon }_0}\frac{1}{r^2}$
$4. \frac{Ze}{4\pi {\epsilon }_0}\frac{r}{R^3}$