When a mass is suspended separately by two different springs, in successive order, then the time period of oscillations is \(t _1\) and \(t_2\) respectively. If it is connected by both springs as shown in the figure below, then the time period of oscillation becomes \(t_0.\) The correct relation between \(t_0,\) \(t_1\) & \(t_2\) is:

1.
2.
3.
4.
1. \(\pm \frac{a}{2}\)
2. \(+a\)
3. \(\pm a\)
4. \(-1\)
The time period of a mass suspended from a spring is \(T\). If the spring is cut into four equal parts and the same mass is suspended from one of the parts, then the new time period will be:
1. \(\frac{T}{4}\)
2. \(T\)
3. \(\frac{T}{2}\)
4. \(2T\)
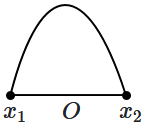
A particle of mass \(m\) oscillates with simple harmonic motion between points \(x_1\) and \(x_2\), the equilibrium position being \(O\). Its potential energy is plotted. It will be as given below in the graph:
| 1. |  |
2. |  |
| 3. |  |
4. |  |
The potential energy of a simple harmonic oscillator, when the particle is halfway to its endpoint, will be:
1. \(\frac{2E}{3}\)
2. \(\frac{E}{8}\)
3. \(\frac{E}{4}\)
4. \(\frac{E}{2}\)
| 1. | \(140 \text{ cm} / \text{s}^2 \) | 2. | \(160 \text{ m} / \text{s}^2 \) |
| 3. | \(140 \text{ m} / \text{s}^2 \) | 4. | \(14 \text{ m} / \text{s}^2\) |
The frequency of a simple pendulum in a free-falling lift will be:
1. zero
2. infinite
3. can't say
4. finite
A spring elongates by a length 'L' when a mass 'M' is suspended to it. Now a tiny mass 'm' is attached to the mass 'M' and then released. The new time period of oscillation will be:
1. \(2 \pi \sqrt{\frac{\left(\right. M + m \left.\right) l}{Mg}}\)
2. \(2 \pi \sqrt{\frac{ml}{Mg}}\)
3. \(2 \pi \sqrt{L / g}\)
4. \(2 \pi \sqrt{\frac{Ml}{\left(\right. m + M \left.\right) g}}\)
| 1. | The value of \(a\) is zero whatever may be the value of \(v\). |
| 2. | When \(v\) is zero, \(a\) is zero. |
| 3. | When \(v\) is maximum, \(a\) is zero. |
| 4. | When \(v\) is maximum, \(a\) is maximum. |
| 1. | \(2n\) | 2. | \(n/2\) |
| 3. | \(n\) | 4. | none of the above |




