Which one of the following statements is true for the speed \(v\) and the acceleration \(a\) of a particle executing simple harmonic motion?
1.
The value of \(a\) is zero whatever may be the value of \(v\).
2.
When \(v\) is zero, \(a\) is zero.
3.
When \(v\) is maximum, \(a\) is zero.
4.
When \(v\) is maximum, \(a\) is maximum.
A spring elongates by a length 'L' when a mass 'M' is suspended to it. Now a tiny mass 'm' is attached to the mass 'M' and then released. The new time period of oscillation will be:
1. \(2 \pi \sqrt{\frac{\left(\right. M + m \left.\right) l}{Mg}}\)
2. \(2 \pi \sqrt{\frac{ml}{Mg}}\)
3. \(2 \pi \sqrt{L / g}\)
4. \(2 \pi \sqrt{\frac{Ml}{\left(\right. m + M \left.\right) g}}\)
The frequency of a simple pendulum in a free-falling lift will be:
1. zero
2. infinite
3. can't say
4. finite
When a mass is suspended separately by two different springs, in successive order, then the time period of oscillations is \(t _1\) and \(t_2\) respectively. If it is connected by both springs as shown in the figure below, then the time period of oscillation becomes \(t_0.\) The correct relation between \(t_0,\) \(t_1\) & \(t_2\) is:

1.
2.
3.
4.
1. \(\pm \frac{a}{2}\)
2. \(+a\)
3. \(\pm a\)
4. \(-1\)
The time period of a mass suspended from a spring is \(T\). If the spring is cut into four equal parts and the same mass is suspended from one of the parts, then the new time period will be:
1. \(\frac{T}{4}\)
2. \(T\)
3. \(\frac{T}{2}\)
4. \(2T\)
A particle of mass \(m\) oscillates with simple harmonic motion between points \(x_1\) and \(x_2\), the equilibrium position being \(O\). Its potential energy is plotted. It will be as given below in the graph:
| 1. |  |
2. | 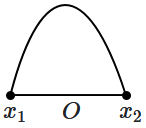 |
| 3. |  |
4. |  |
The potential energy of a simple harmonic oscillator, when the particle is halfway to its endpoint, will be:
1. \(\frac{2E}{3}\)
2. \(\frac{E}{8}\)
3. \(\frac{E}{4}\)
4. \(\frac{E}{2}\)
| 1. | \(140 \text{ cm} / \text{s}^2 \) | 2. | \(160 \text{ m} / \text{s}^2 \) |
| 3. | \(140 \text{ m} / \text{s}^2 \) | 4. | \(14 \text{ m} / \text{s}^2\) |
| 1. | \(2n\) | 2. | \(n/2\) |
| 3. | \(n\) | 4. | none of the above |






