For rocket propulsion, the velocity of exhaust gases relative to the rocket is \(2\) km/s. If the mass of a rocket system is \(1000\) kg, then the rate of fuel consumption for the rocket to rise with an acceleration \(4.9\) m/s2 will be:
1. \(12.25~\text{kg}/\text{s}\)
2. \(17.5~\text{kg}/\text{s}\)
3. \(7.35~\text{kg}/\text{s}\)
4. \(5.2~\text{kg}/\text{s}\)
1. \(12.25~\text{kg}/\text{s}\)
2. \(17.5~\text{kg}/\text{s}\)
3. \(7.35~\text{kg}/\text{s}\)
4. \(5.2~\text{kg}/\text{s}\)
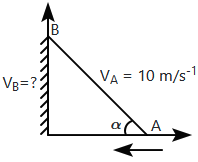
A rigid rod is placed against the wall as shown in the figure. When the velocity at its lower end is \(10\) ms-1 and its base makes an angle \(\alpha=60^\circ\) with horizontal, then the vertical velocity of its end \(\mathrm{B}\) (in ms-1) will be:
| 1. | \(10\sqrt{3}\) | 2. | \(\frac{10}{\sqrt{3}}\) |
| 3. | \(5\sqrt{3}\) | 4. | \(\frac{5}{\sqrt{3}}\) |
If \(100\) N force is applied to \(10\) kg block as shown in diagram, then the acceleration produced for the slab will be:

| 1. | \(1. 65 \) m/s2 | 2. | \(0.98 \) m/s2 |
| 3. | \(1. 2 \) m/s2 | 4. | \(0.25\) m/s2 |
A block of mass \(m\) is placed on a smooth wedge of inclination \(\theta\). The whole system is accelerated horizontally so that the block does not slip on the wedge. The force exerted by the wedge on the block (\(g\) is the acceleration due to gravity) will be:
1. \(mg~\mathrm{sin\theta}\)
2. \(mg\)
3. \(\frac{mg}{\mathrm{cos\theta}}\)
4. \(mg~\mathrm{cos\theta}\)
The coefficient of static friction, \(\mu_s,\) between block A of mass \(2\) kg and the table as shown in the figure is \(0.2\). What would be the maximum mass value of block B so that the two blocks do not move? The string and the pulley are assumed to be smooth and massless. (Take \(g=10\) m/s2 )
1. \(4.0\) kg
2. \(0.2\) kg
3. \(0.4\) kg
4. \(2.0\) kg
An object of mass \(3\) kg is at rest. Now if a force of \(\overrightarrow{F} = 6 t^{2} \hat{i} + 4 t \hat{j}\) is applied to the object, then the velocity of the object at \(t =3\) second will be:
1. \(18 \hat{i} + 3 \hat{j}\)
2. \(18 \hat{i} + 6 \hat{j}\)
3. \(3 \hat{i} + 18 \hat{j}\)
4. \(18 \hat{i} + 4 \hat{j}\)
A block of mass 10 kg is placed on a rough horizontal surface with a coefficient of friction µ = 0.5. If a horizontal force of 100 N acts on the block, then the acceleration of the block will be:
1. 10 m/s2
2. 5 m/s2
3. 15 m/s2
4. 0.5 m/s2
If a lift of mass 1000 Kg is moving with an acceleration of 1 m/s2 in an upward direction, then the tension developed in the string that is connected to the lift is:
1. 9800 N
2. 10, 800 N
3. 11000 N
4. 10, 000 N
A cricketer catches a ball of mass \(150~\mathrm{gm}\) in \(0.1\) \(\mathrm{s}\) moving with a speed of \(20~\mathrm{ms^{-1}}\). Then he experiences a force of:
1. \(300~\mathrm{N}\)
2. \(30~\mathrm{N}\)
3. \(3~\mathrm{N}\)
4. \(0.3~\mathrm{N}\)
On the horizontal surface of a truck, a block of mass \(1\) kg is placed (\(\mu = 0.6\)) and the truck is moving with an acceleration of \(5\) m/s2. The frictional force on the block will be:
1. \(5\) N
2. \(6\) N
3. \(5.88\) N
4. \(8\) N