+91-8527521718
Signup | Login
  • 1(current)
Q. No.
A particle \((P)\) of mass \(m\) is placed on the axis of a uniform circular ring of radius \(R\) and mass \(M.\) Its distance \((OP)\) from the centre \((O)\) of the ring is equal to \(R.\) Let the net gravitational field at the centre of the ring be \(g.\) Then, the gravitational potential energy of the interaction of the system is:
         

1. \(-MgR\)
2. \(-mgR\)
3. \(\dfrac{-MgR}{\sqrt2}\)
4. \(\dfrac{-mgR}{\sqrt2}\)
Subtopic:  Electric Potential Energy |
Level 3: 35%-60%

To unlock all the explanations of this course, you need to be enrolled.

Hints

To unlock all the explanations of this course, you need to be enrolled.

Match the charge distribution mentioned in Column I with the graph of corresponding potential energy of interaction under Column II.
Column I
Charge distribution		 Column II
Interaction energy
\(\mathrm{(A)}\)  
Two point charges separated by distance \(x\)		 \(\mathrm{(I)}\)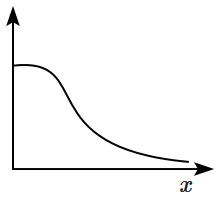  
\(\mathrm{(B)}\)  
Interaction energy of a point charge with a uniformly charged spherical surface		 \(\mathrm{(II)}\)  
\(\mathrm{(C)}\)
Interaction energy of a point charge with a uniform spherical volume charge		 \(\mathrm{(III)}\)
\(\mathrm{(D)}\)
Interaction energy of a dipole & a point charge		 \(\mathrm{(IV)}\)
 
1. \(\mathrm{A\text-II,B\text-I,C\text-IV,D\text-II}\)
2. \(\mathrm{A\text-II,B\text-IV,C\text-II,D\text-III}\)
3. \(\mathrm{A\text-II,B\text-II,C\text-II,D\text-IV}\)
4. \(\mathrm{A\text-II,B\text-IV,C\text-I,D\text-III}\)
Subtopic:  Electric Potential Energy |
 85%
Level 1: 80%+

To unlock all the explanations of this course, you need to be enrolled.

Hints

To unlock all the explanations of this course, you need to be enrolled.

A uniformly charged metallic sphere holds a total charge \(Q_0\) and has a potential \(V_0.\) The total potential energy stored is:
1. \(Q_0V_0\) 2. \(\dfrac{Q_0V_0}{2}\)
3. \(\dfrac{Q_0V_0}{4}\) 4. \(-Q_0V_0\)
Subtopic:  Electric Potential Energy |
 62%
Level 2: 60%+

To unlock all the explanations of this course, you need to be enrolled.

Hints

To unlock all the explanations of this course, you need to be enrolled.

advertisementadvertisement
Four identical point charges \(q,\) each are fixed at the corners of a square of side \(a.\) The work done in bringing a point charge \(q,\) from infinity and placing it at the centre of the square is: \(\left(k=\dfrac{1}{4\pi\varepsilon_0}\right)\)
1. \(k.\dfrac{4q^2}{a}\) 2. \(k.\dfrac{4\sqrt2q^2}{a}\)
3. \(k.\dfrac{4q^2}{a\sqrt2}\) 4. zero
Subtopic:  Electric Potential Energy |
 62%
Level 2: 60%+

To unlock all the explanations of this course, you need to be enrolled.

Hints

To unlock all the explanations of this course, you need to be enrolled.

A particle of charge \(q,\) mass \(m\) falls under gravity starting from rest. It falls through a height \(H,\) while being acted upon by an electric field, in addition to gravity. At the end of its motion, it briefly comes to rest. The potential difference between the two extreme points of its motion is:
1. \(\dfrac{mgH}{q}\) 2. \(\dfrac{2mgH}{q}\)
3. \(\dfrac{mgH}{2q}\) 4. zero
Subtopic:  Electric Potential Energy |
 62%
Level 2: 60%+

To unlock all the explanations of this course, you need to be enrolled.

Hints

To unlock all the explanations of this course, you need to be enrolled.

A pair of identical point charges (\(q\)-each) are placed at the two vertices of an equilateral triangle. What charge \((Q)\) should be placed at the third vertex, so that the potential energy of the charge distribution is doubled?
      
1. \(q\) 2. \(\Large\frac{q}{2}\)
3. \(2q\) 4. \(4q\)
Subtopic:  Electric Potential Energy |
 63%
Level 2: 60%+

To unlock all the explanations of this course, you need to be enrolled.

Hints

To unlock all the explanations of this course, you need to be enrolled.

advertisementadvertisement
A point charge \(q\) is placed at the centre of a uniformly charged ring of radius \(R,\) carrying a charge \(Q. \) The potential energy of interaction between them is: \(\left(k={\Large\frac{1}{4\pi\varepsilon_0}}\right)\)
1. \(k{\Large\frac{qQ}{R}}\) 2. \(k{\Large\frac{qQ}{2\pi R}}\)
3. \(k{\Large\frac{\pi qQ}{R}}\) 4. zero
Subtopic:  Electric Potential Energy |
 71%
Level 2: 60%+

To unlock all the explanations of this course, you need to be enrolled.

Hints

To unlock all the explanations of this course, you need to be enrolled.

The work done by electric field in taking a point charge \((q),\) from the centre \((O)\) of a uniformly charged, thin hemispherical shell (charge: \(Q\)) to a point \(A,\) along the path shown in the figure, is: \(\left(k={\Large\frac{1}{4\pi\varepsilon_0}},OA=3R\right)\)
                   
1. zero
2. \(\Large\frac{kqQ}{3R}\)
3. \(\Large\frac{2kqQ}{3R}\)
4. none of the above
Subtopic:  Electric Potential Energy |
 64%
Level 2: 60%+

To unlock all the explanations of this course, you need to be enrolled.

Hints

To unlock all the explanations of this course, you need to be enrolled.

  • 1(current)
Q. No.

NEET Information

courses

Company

Botany Questions

Chemistry Questions

Physics Questions

Zoology Questions

© 2025 GoodEd Technologies Pvt. Ltd.