Q. No.A pendulum made of a uniform wire of cross-sectional area \(A\) has time period \(T\). When an additional mass \(M\) is added to its bob, the time period changes to \(T_M\). If the Young’s modulus of the material of the wire is \(Y\) then \(\frac{1}{Y}\) is equal to:
(\(g=\) gravitational acceleration)
1. \( \left[\left(\frac{{T}_{{M}}}{{T}}\right)^2-1\right] \frac{{Mg}}{{A}} \)
2. \(\left[1-\left(\frac{{T}_{{M}}}{{T}}\right)^2\right] \frac{{A}}{{Mg}} \)
3. \(\left[1-\left(\frac{{T}}{{T}_{{M}}}\right)^2\right] \frac{{A}}{{Mg}} \)
4. \(\left[\left(\frac{{T}_{{M}}}{{T}}\right)^2-1\right] \frac{{A}}{{Mg}}\)
For a simple pendulum, a graph is plotted between its kinetic energy (\(KE\)) and potential energy (\(PE\)) against its displacement \(d\). Which one of the following represents these correctly? (graphs are schematic and not drawn to scale)
| 1. |  |
2. |  |
| 3. |  |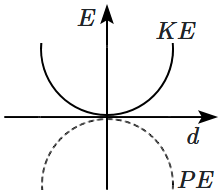
4. |  |
A simple pendulum has a time period \(T\) in air. The bob is then completely immersed and continues to oscillate freely in a non-viscous liquid whose density is \(\left ( \dfrac{1}{16}\right )^\mathrm{th}
\) of that of the bob. Assuming no damping and only the effect of buoyancy, what is the new time period of oscillation?
1. \( 2 T \sqrt{\dfrac{1}{14}} \)
2. \( 2 T \sqrt{\dfrac{1}{10}} \)
3. \(4 T \sqrt{\dfrac{1}{15}} \)
4. \( 4 T \sqrt{\dfrac{1}{14}} \)
1. \(\dfrac{3k\theta_0^2}{l}\)
2. \(\dfrac{2k\theta_0^2}{l}\)
3. \(\dfrac{k\theta_0^2}{l}\)
4. \(\dfrac{k\theta_0^2}{2l}\)
A ring is hung on a nail. It can oscillate, without slipping or sliding (i) in its plane with a time period \(T_1\) and, (ii) back and forth in a direction perpendicular to its plane, with a period \(T_2\). The ratio \(\frac{T_1}{T_2}\) will be:
1. \(\frac{2}{\sqrt{3}} \)
2. \(\frac{\sqrt{2}}{3} \)
3. \( \frac{2}{3} \)
4. \(\frac{3}{\sqrt{2}}\)
If the time period of a \(2\) m long simple pendulum is \(2\) s, the acceleration due to gravity at the place where the pendulum is executing simple harmonic motion is:
1. \(\pi^{2}\) m/s2
2. \(2\pi^{2}\) m/s2
3. \(9.8\) m/s2
4. \(16\) m/s2
Given below are two statements:
| Statement I: | A seconds pendulum has a time period of \(1\) second. |
| Statement II: | A seconds pendulum takes exactly \(1\) second to travel between its two extreme positions. |
| 1. | Both Statement I and Statement II are incorrect. |
| 2. | Statement I is incorrect and Statement II is correct. |
| 3. | Statement I is correct and Statement II is incorrect. |
| 4. | Both Statement I and Statement II are correct. |
| 1. | \(\sqrt{\dfrac{6}{5}} ~T \) | 2. | \(\sqrt{\dfrac{5}{6}} ~T\) |
| 3. | \(\sqrt{\dfrac{6}{7}}~T\) | 4. | \(\sqrt{\dfrac{7}{6}} ~T\) |
\({y}={A} \sin (\pi {t}+\phi),\) where time is measured in seconds. The length of the pendulum is:
1. \(97.23~\text{cm}\)
2. \(25.3~\text{cm}\)
3. \(99.4~\text{cm}\)
4. \(406.1~\text{cm}\)
(Given \(R=\) The radius of the earth and acceleration due to gravity at the surface of the earth \(g = \pi^2 ~\text{m/s}^2\))
| 1. | \({\dfrac 2 9} ~\text m\) | 2. | \({\dfrac 4 9} ~\text m\) |
| 3. | \({\dfrac 8 9} ~\text m\) | 4. | \({\dfrac 1 9} ~\text m\) |
© 2025 GoodEd Technologies Pvt. Ltd.