The radius of the circle, the period of revolution, initial position and direction of revolution are indicated in the figure.
The \(y\)-projection of the radius vector of rotating particle \(P\) will be:
| 1. | \(y(t)=3 \cos \left(\dfrac{\pi \mathrm{t}}{2}\right)\), where \(y\) in m |
| 2. | \(y(t)=-3 \cos 2 \pi t\) , where \(y\) in m |
| 3. | \(y(t)=4 \sin \left(\dfrac{\pi t}{2}\right)\), where \(y\) in m |
| 4. | \(y(t)=3 \cos \left(\dfrac{3 \pi \mathrm{t}}{2}\right) \), where \(y\) in m |
The figure shows the circular motion of a particle. The radius of the circle, the period, the sense of revolution, and the initial position are indicated in the figure. The simple harmonic motion of the \({x\text-}\)projection of the radius vector of the rotating particle \(P\) will be:

1. \(x \left( t \right) = B\text{sin} \left(\dfrac{2 πt}{30}\right)\)
2. \(x \left( t \right) = B\text{cos} \left(\dfrac{πt}{15}\right)\)
3. \(x \left( t \right) = B\text{sin} \left(\dfrac{πt}{15} + \dfrac{\pi}{2}\right)\) \(\)
4. \(x \left( t \right) = B\text{cos} \left(\dfrac{πt}{15} + \dfrac{\pi}{2}\right)\)
The figure given below depicts two circular motions. The radius of the circle, the period of revolution, the initial position, and the sense of revolution are indicated in the figures. Equations of the \(x\)-projection of the radius vector of the rotating particle \(\mathrm P\) in each case are, respectively:
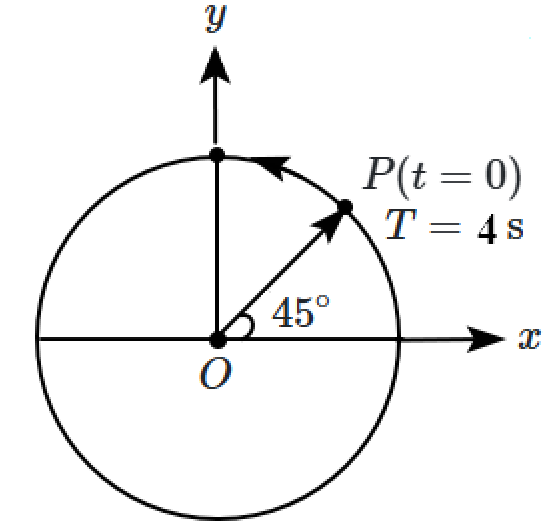
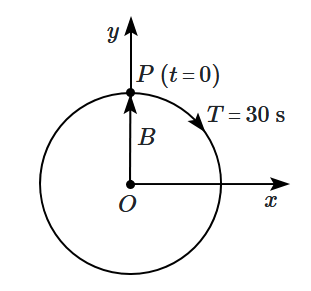
| 1. | \(\small{x}({t})={A} \cos \left(\dfrac{2 \pi}{4} {t}+\dfrac{\pi}{4}\right)\text{ and }{x}({t})={B} \cos \left(\dfrac{\pi}{15} {t}-\dfrac{\pi}{2}\right)\) |
| 2. | \(\small{x}({t})={A} \cos \left(\dfrac{2 \pi}{4} {t}+\dfrac{\pi}{4}\right)\text{ and }{x}({t})={B} \sin \left(\dfrac{\pi}{15} {t}-\dfrac{\pi}{2}\right)\) |
| 3. | \(\small{x}({t})={A} \cos \left(\dfrac{2 \pi}{4} {t}+\dfrac{\pi}{4}\right)\text{ and }{x}({t})={B} \cos \left(\dfrac{\pi}{15} {t}-\dfrac{\pi}{4}\right)\) |
| 4. | \(\small{x}({t})={A} \sin \left(\dfrac{2 \pi}{4} {t}+\dfrac{\pi}{4}\right)\text{ and }{x}({t})={B} \cos \left(\dfrac{\pi}{15} {t}-\dfrac{\pi}{2}\right)\) |



