- 1(current)
Q. No.When a rubber band is stretched by a distance \(x,\) it exerts a restoring force given by; \(F=(ax+bx^2),\) where \(a\) and \(b\) are constants. What is the total work done in stretching the rubber band from its natural (unstretched) length to a length \(L\text{?}\)
| 1. | \(\dfrac{1}{2}(aL^2+bL^3)\) | 2. | \(\left ( \dfrac{aL^2}{2}+\dfrac{bL^3}{3} \right ) \) |
| 3. | \(\dfrac{1}{2}\left(\dfrac{aL^2}{2}+\dfrac{bL^3}{3}\right) \) | 4. | \((aL^2+bL^3)\) |
Subtopic: Work Done by Variable Force |
79%
From NCERT
Please attempt this question first.
Hints
Please attempt this question first.
A person pushes a box on a rough horizontal plateform surface. He applies a force of \(200~\text{N}\) over a distance of \(15~\text{m}\). Thereafter, he gets progressively tired and his applied force reduces linearly with distance to \(100~\text{N}\). The total distance through which the box has been moved is \(30~\text{m}\). What is the work done by the person during the total movement of the box?
1. \(5690~\text{J}\)
2. \(3280~\text{J}\)
3. \(2780~\text{J}\)
4. \(5250~\text{J}\)
Subtopic: Work Done by Variable Force |
50%
From NCERT
JEE
Please attempt this question first.
Hints
Please attempt this question first.
Arrange the four graphs in descending order of total work done; where \(W_1, W_2, W_3 ~\text{and}~W_4\) are the work done corresponding to figures \(a,b,c~\text{and}~d\) respectively.
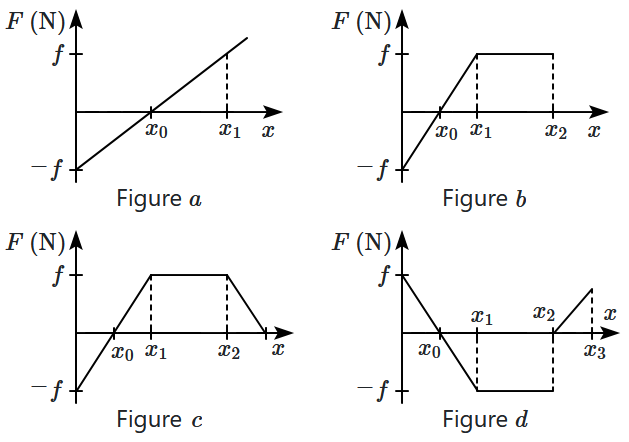
| 1. | \( W_3>W_2>W_1>W_4 \) |
| 2. | \( W_3>W_2>W_4>W_1 \) |
| 3. | \({W}_2>{W}_3>{W}_4>{W}_1 \) |
| 4. | \(W_2>W_3>W_1>W_4\) |
Subtopic: Work Done by Variable Force |
71%
From NCERT
JEE
Please attempt this question first.
Hints
Please attempt this question first.
A particle of mass \(500\) g is moving in a straight line with velocity \(v=b x^{5 / 2}\). The work done by the net force during its displacement from \(x = 0\) to \(x=4\) m is:
(Take \(b=0.25\) m–3/2 s–1)
(Take \(b=0.25\) m–3/2 s–1)
| 1. | \(2\) J | 2. | \(4\) J |
| 3. | \(8\) J | 4. | \(16\) J |
Subtopic: Work Done by Variable Force |
61%
From NCERT
JEE
Please attempt this question first.
Hints
Please attempt this question first.
If a force \(F\) applied on an object moving along the \(\mathrm{y}\)-axis varies with the y-coordinate as \(F=3+2y^{2}. \) The work done in displacing the body from \(y=2\) m to \(y=5\) m is:
1. \(87\) J
2. \(0 \)
3. \(57\) J
4. \(72\) J
1. \(87\) J
2. \(0 \)
3. \(57\) J
4. \(72\) J
Subtopic: Work Done by Variable Force |
83%
From NCERT
JEE
Please attempt this question first.
Hints
Please attempt this question first.
Force acting on a particle moving along \(\mathrm{x \text-\text{axis}} \) is given by, \(\overrightarrow{F}=(2+3 x) \hat{i}\). The work done by this force from \(x = 0\) to \(x = 4 ~\text{m}\) is:
| 1. | \(16 \) J | 2. | \(32 \) J |
| 3. | \(4 \) J | 4. | \(8 \) J |
Subtopic: Work Done by Variable Force |
85%
From NCERT
JEE
Please attempt this question first.
Hints
Please attempt this question first.
A variable force given by; \(F=5kx \) (in newtons) acts on a body moving along the \(x\)-axis, where \(k\) is a constant.
What is the work done by this force as the body moves from \(x=2~\text{m}\) to \(x=5~\text{m}\)?
What is the work done by this force as the body moves from \(x=2~\text{m}\) to \(x=5~\text{m}\)?
| 1. | \(\left ( \dfrac{205}{2}k \right )\text{J} \) | 2. | \(\left ( \dfrac{105}{2}k \right )\text{J} \) |
| 3. | \((52k)~\text{J}\) | 4. | \((51k)~\text{J}\) |
Subtopic: Work Done by Variable Force |
74%
From NCERT
Please attempt this question first.
Hints
Please attempt this question first.
A particle of mass m moves on a straight line with its velocity increasing with distance according to the equation \(\begin{equation} v=\alpha \sqrt{x} \end{equation}\), where \(\begin{equation} \alpha \end{equation}\) is a constant. The total work done by all the forces applied on the particle during its displacement from \(x=0\) to \(x=d\), will be :
1. \(\begin{equation} \frac{m}{2 \alpha^2 d} \end{equation}\)
2. \(\begin{equation} \frac{m d}{2 \alpha^2} \end{equation}\)
3. \(\begin{equation} \frac{m \alpha^2 d}{2} \end{equation}\)
4. \(\begin{equation} 2 m \alpha^2 d \end{equation}\)
1. \(\begin{equation} \frac{m}{2 \alpha^2 d} \end{equation}\)
2. \(\begin{equation} \frac{m d}{2 \alpha^2} \end{equation}\)
3. \(\begin{equation} \frac{m \alpha^2 d}{2} \end{equation}\)
4. \(\begin{equation} 2 m \alpha^2 d \end{equation}\)
Subtopic: Work Done by Variable Force |
81%
Please attempt this question first.
Hints
Please attempt this question first.
- 1(current)
Q. No.
© 2025 GoodEd Technologies Pvt. Ltd.