A long cylindrical shell is uniformly charged such that the upper half of its curved surface carries a positive surface charge density \(\sigma,\) while the lower half carries an equal negative surface charge density \(-\sigma.\) Which of the following schematic diagrams (not drawn to scale) most accurately represents the resulting pattern of electric field lines around the cylinder?
| 1. | 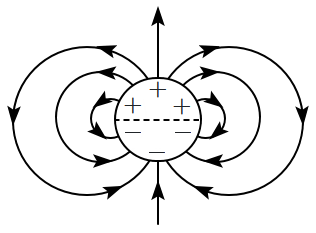 |
| 2. |  |
| 3. |  |
| 4. | 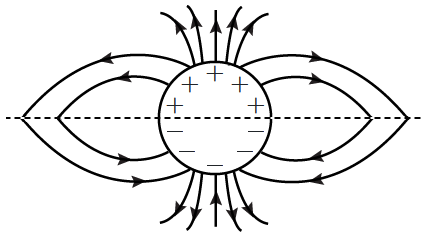 |
1. \(\dfrac{\sigma h}{2a~\epsilon_0}\)
2. \(\dfrac{\sigma h}{4a~\epsilon_0}\)
3. \(\dfrac{\sigma h}{8a~\epsilon_0}\)
4. \(\dfrac{\sigma h}{a~\epsilon_0}\)

1. \({(50\times10^3~\text{N/C})~\hat{j}}\)
2. \({(50\times10^3~\text{N/C})~\hat{i}}\)
3. \({(25\times10^3~\text{N/C})~\hat{j}}\)
4. \({(25\times10^3~\text{N/C})~\hat{i}}\)
The region between two concentric spheres of radii '\(a\)' and '\(b\)' , respectively (see figure), has volume charge density \(\rho=\frac{A}{r}\), where \(A\) is a constant and \(r\) is the distance from the centre. At the centre of the spheres is a point charge \(Q\). The value of \(A\) such that the electric field in the region between the spheres will be constant, is:
1. \( \frac{Q}{2 \pi a^2} \)
2. \(\frac{Q}{2 \pi\left(b^2-a^2\right)} \)
3. \(\frac{2 Q}{\pi\left(a^2-b^2\right)} \)
4. \(\frac{2 Q}{\pi a^2}\)
An electric dipole with dipole moment \(\vec p,\) inclined at an angle \(\theta\) to the \(x\text-\)axis, experiences a torque \(\vec{\tau_1}= \tau \hat k\) in the field \(\vec E_1= E \hat i,\) and a torque \(\vec{\tau_2}=-\vec{\tau_1}\) in the field \(\vec E_2 = \sqrt{3}E \hat j.\) The angle \(\theta\) is:
| 1. | \(30^{\circ}\) | 2. | \(45^{\circ}\) |
| 3. | \(60^{\circ}\) | 4. | \(90^{\circ}\) |

Let the respective electric fluxed through the surfaces be \(\phi_1,\phi_2,\phi_3\) and \(\phi_4.\) Then:
1. \(\phi_1=\phi_2=\phi_3=\phi_4 \)
2. \(\phi_1>\phi_3;~\phi_2<\phi_4 \)
3. \(\phi_1>\phi_2>\phi_3>\phi_4 \)
4. \(\phi_1<\phi_2=\phi_3>\phi_4 \)
| 1. |  |
3. |  |
| 2. |  |
4. |  |

2. \(\dfrac{Q}{2{\epsilon_0}}\)
3. \(\dfrac{Q}{3{\epsilon_0}}\)
4. \(\dfrac{Q}{{\epsilon_0}}\)
1. \(\dfrac{3F}{4}\)
2. \(\dfrac{F}{2}\)
3. \(\dfrac{3F}{8}\)
4. \(F\)
The bob of a simple pendulum has mass \(2~\text{g}\) and a charge of \(5.0~\mu \text{C}\). It is at rest in a uniform horizontal electric field of intensity \(2000~\text{V/m}\). At equilibrium, the angle that the pendulum makes with the vertical is: (take \(g = 10~\text{m/s}^2\))
1. \( \tan ^{-1}(5.0) \)
2. \( \tan ^{-1}(0.5) \)
3. \( \tan ^{-1}(0.2) \)
4. \( \tan ^{-1}(2.0)\)







