The region between two concentric spheres of radii '\(a\)' and '\(b\)' , respectively (see figure), has volume charge density \(\rho=\frac{A}{r}\), where \(A\) is a constant and \(r\) is the distance from the centre. At the centre of the spheres is a point charge \(Q\). The value of \(A\) such that the electric field in the region between the spheres will be constant, is:
1. \( \frac{Q}{2 \pi a^2} \)
2. \(\frac{Q}{2 \pi\left(b^2-a^2\right)} \)
3. \(\frac{2 Q}{\pi\left(a^2-b^2\right)} \)
4. \(\frac{2 Q}{\pi a^2}\)

Let the respective electric fluxed through the surfaces be \(\phi_1,\phi_2,\phi_3\) and \(\phi_4.\) Then:
1. \(\phi_1=\phi_2=\phi_3=\phi_4 \)
2. \(\phi_1>\phi_3;~\phi_2<\phi_4 \)
3. \(\phi_1>\phi_2>\phi_3>\phi_4 \)
4. \(\phi_1<\phi_2=\phi_3>\phi_4 \)

2. \(\dfrac{Q}{2{\epsilon_0}}\)
3. \(\dfrac{Q}{3{\epsilon_0}}\)
4. \(\dfrac{Q}{{\epsilon_0}}\)
A point charge of \(+12~\mathrm{\mu C}\) is at a distance \(6\) cm vertically above the centre of a square of side \(12\) cm as shown in figure. The magnitude of the electric flux through the square will be:
1. \( 226 \times 10^2 ~\frac{\mathrm{Nm}^2}{\mathrm{C}}\)
2. \( 226 \times 10^3 ~\frac{\mathrm{Nm}^2}{\mathrm{C}}\)
3. \(326 \times 10^3 ~\frac{\mathrm{Nm}^2}{\mathrm{C}}\)
4. \( 326 \times 10^2 ~\frac{\mathrm{Nm}^2}{\mathrm{C}}\)
A point charge \(q\) is placed at one corner of a cube, as shown in the figure. What is the electric flux through the shaded area?

| 1. | \(\dfrac{q}{4\varepsilon_0}\) | 2. | \(\dfrac{q}{24\varepsilon_0}\) |
| 3. | \(\dfrac{q}{48\varepsilon_0}\) | 4. | \(\dfrac{q}{8\varepsilon_0}\) |
Given below are two statements :
| Statement I: | An electric dipole is placed at the centre of a hollow sphere. The flux of the electric field through the sphere is zero but the electric field is not zero anywhere in the sphere. |
| Statement II: | If \(R\) is the radius of a solid metallic sphere and \(Q\) be the total charge on it. The electric field at any point on the spherical surface of radius \(r~(<R)\) is zero but the electric flux passing through this closed spherical surface of radius \(r\) is not zero. |
| 1. | Both Statement I and Statement II are true |
| 2. | Statement I is true but Statement II is false |
| 3. | Both Statement I and Statement II are false |
| 4. | Statement I is false but Statement II is true. |

1. \({E}_1=\dfrac{\sigma}{\varepsilon_0}, {E}_2=\dfrac{\sigma}{ 2 \varepsilon_0}\)
2. \({E}_1=\dfrac{2 \sigma}{\varepsilon_0}, {E}_2=\dfrac{\sigma}{ \varepsilon_0} \)
3. \({E}_1={E}_2=\dfrac{\sigma} {2 \varepsilon_0} \)
4. \({E}_1={E}_2=\dfrac{\sigma}{\varepsilon_0}\)
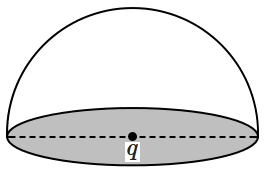
| 1. | \(\dfrac{q}{\varepsilon_0} \) | 2. | \( \dfrac{q}{2 \varepsilon_0} \) |
| 3. | \(\dfrac{q}{4 \varepsilon_0} \) | 4. | \(\dfrac{q}{2 \pi \varepsilon_0}\) |

| 1. | \(1~\text{Vm}^{-1}\) | 2. | \(2~\text{Vm}^{-1}\) |
| 3. | \(3~\text{Vm}^{-1}\) | 4. | \(4~\text{Vm}^{-1}\) |
\(\rho(r)= \begin{cases}\rho_0\left(\frac{3}{4}-\frac{r}{R}\right) & \text { for } r \leq R \\ \text { Zero } & \text { for } r>R\end{cases}\)
where \(r(r<R)\) is the distance from the centre \(O\) (as shown in the figure). The electric field at point \(P\) will be:

1. \(\frac{\rho_0 {r}}{4 \varepsilon_0}\left(\frac{3}{4}-\frac{r}{R}\right) \)
2. \(\frac{\rho_0 {r}}{3 \varepsilon_0}\left(\frac{3}{4}-\frac{{r}}{R}\right) \)
3. \(\frac{\rho_0{r}}{4 \varepsilon_0}\left(1-\frac{{r}}{{R}}\right) \)
4. \(\frac{\rho_0 r}{5 \varepsilon_0}\left(1-\frac{r}{R}\right)\)








