A long cylindrical shell is uniformly charged such that the upper half of its curved surface carries a positive surface charge density \(\sigma,\) while the lower half carries an equal negative surface charge density \(-\sigma.\) Which of the following schematic diagrams (not drawn to scale) most accurately represents the resulting pattern of electric field lines around the cylinder?
| 1. | 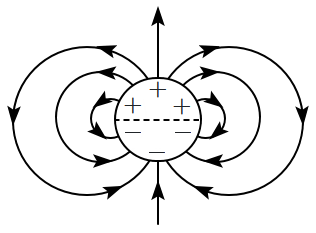 |
| 2. |  |
| 3. |  |
| 4. | 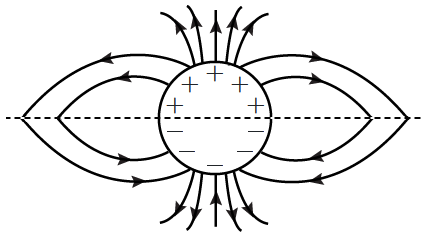 |
1. \(\dfrac{\sigma h}{2a~\epsilon_0}\)
2. \(\dfrac{\sigma h}{4a~\epsilon_0}\)
3. \(\dfrac{\sigma h}{8a~\epsilon_0}\)
4. \(\dfrac{\sigma h}{a~\epsilon_0}\)

1. \({(50\times10^3~\text{N/C})~\hat{j}}\)
2. \({(50\times10^3~\text{N/C})~\hat{i}}\)
3. \({(25\times10^3~\text{N/C})~\hat{j}}\)
4. \({(25\times10^3~\text{N/C})~\hat{i}}\)
| 1. |  |
3. |  |
| 2. |  |
4. |  |
The bob of a simple pendulum has mass \(2~\text{g}\) and a charge of \(5.0~\mu \text{C}\). It is at rest in a uniform horizontal electric field of intensity \(2000~\text{V/m}\). At equilibrium, the angle that the pendulum makes with the vertical is: (take \(g = 10~\text{m/s}^2\))
1. \( \tan ^{-1}(5.0) \)
2. \( \tan ^{-1}(0.5) \)
3. \( \tan ^{-1}(0.2) \)
4. \( \tan ^{-1}(2.0)\)
Four point charges \(-q\), \(+q\), \(+q\) and \(-q\) are placed on \(y\)-axis at \(y=-2d\), \(y=-d\), \(y=+d\), \(y=+2d\), respectively. The magnitude of the electric field \(E\) at a point a the \(x\)-axis at \(x=D\), with \(D>>d\), will behave as:
1. \( E \propto \frac{1}{D} \)
2. \( E \propto \frac{1}{D^3} \)
3. \( E \propto \frac{1}{D^4} \)
4. \( E \propto \frac{1}{D^2}\)
A simple pendulum of length \(L\) is suspended between the plates of a parallel-plate capacitor producing a uniform electric field \(E,\) as shown in the figure. The bob has a mass \(m\) and a charge \(q.\) The time period of oscillation of the pendulum is given by:
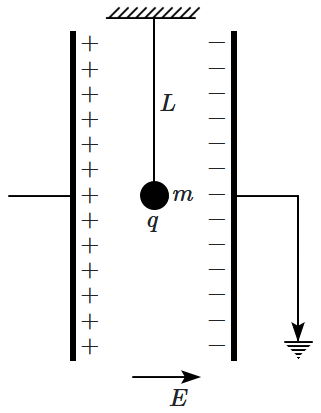
| 1. | \( 2 \pi \sqrt{\dfrac{L}{\sqrt{{g}^2-\dfrac{{q}^2 {E}^2}{~{m}^2}}}} \) | 2. | \(2\pi\sqrt{\dfrac{L}{\sqrt{({g}+\dfrac{qE}{m})}}}\) |
| 3. | \(2 \pi \sqrt{\dfrac{{L}}{\sqrt{{g}-\dfrac{{qE}}{m}}}} \) | 4. | \( 2 \pi \sqrt{\dfrac{{L}}{\sqrt{{g}^2+\left(\dfrac{{qE}}{{m}}\right)^2}}} \) |
Shown in the figure is a shell made of a conductor. It has inner radius \(a\) and outer radius \(b\), and carries charge \(Q\). At its centre is a dipole \(\vec{p}\) as shown. In this case:
| 1. | surface charge density on the inner surface is uniform and equal to \(\frac{(Q/2)}{4\pi a^2}\) |
| 2. | surface charge density on the outer surface depends on \(|\vec{p}|\) |
| 3. | surface charge density on the inner surface of the shell is zero everywhere |
| 4. | the electric field outside the shell is the same as that of a point charge at the centre of the shell |
1. \(\dfrac {{R}}{ \sqrt{5}}\)
2. \(\dfrac {{R}}{ \sqrt{2}}\)
3. \({{R}}\)
4. \( {{R}}{ \sqrt{2}}\)
\((\text{take} ~{1 \over 4 \pi \varepsilon_0}=9 \times 10^9~\text{Nm}^2\text{C}^{-2})\)
1. \((63 \hat{{i}}-27 \hat{{i}})\times 10^2\)
2. \((-63 \hat{{i}}+27 \hat{{i}})\times 10^2\)
3. \((81 \hat{{i}}-81 \hat{{i}})\times 10^2\)
4. \((-81 \hat{{i}}+81 \hat{{i}})\times 10^2\)







