Q. No.| a. | \( \small{n=3, \ell=2, m=0, s=\frac{-1}{2} \,\& \ \,n=3, \ell=2, m=-1, s=\frac{+1}{2}}\) |
| b. | \(\small{n=2, \ell=1, m=1 , \ s=\frac{-1}{2}\, \&\, \ n=3, \ell=1, m=1 \mathrm{~s}=\frac{+1}{2}}\) |
| c. | \(\small{n=4, \ell=2, m=-1, s=\frac{1}{2}\, \&\, \ n=3, \ell=2, m=-1, s=\frac{1}{2}}\) |
1. a
2. b
3. c
4. a, b
Given: \(h = 6.62 \times 10^{-34} \mathrm{~J} \ \mathrm{sec}, \mathrm{c}=3 \times 10^{8} \mathrm{~m \ s}^{-1}\)
1. \(2 \times 10^5 J/mol\)
2. \(6.64 \times 10^8 J/mol\)
3. \(1.24 \times 10^4 J/mol\)
4. \(1.24 \times 10^8 J/mol\)
[given: \(h = 6.6 \times 10^{-34} J sec\)]
1. \(9.24 \times 10^{-19}J \)
2. \(9.24 \times 10^{-18}J \)
3. \(4.62 \times 10^{-19}J \)
4. \(4.62 \times 10^{-18}J \)
| (i). | n (principal quantum number) can have values 1, 2, 3, 4, ....... |
| (ii). | The number of orbitals for a given value of l is (2l+1). |
| (iii). | The value of spin quantum numbers is always \(\pm\frac12\). |
| (iv). | For l=5, the total number of orbitals is 9. |
1. (i), (ii), (iii)
2. (i), (ii), (iv)
3. (i), (ii), (iii), (iv)
4. (i), (iii), (iv)
The plots of radial distribution functions for various orbitals of hydrogen atom against 'r' are given below:
a.
b.
c.
d.
The correct plot for 3s orbital is:
1. (B)
2. (A)
3. (D)
4. (C)
A proton and a Li3+ nucleus are accelerated by the same potential. If Li3+ and denote the de-Broglie wavelengths of Li3+ and proton respectively, then the value of \(\frac{\lambda _{Li^{3+}}}{\lambda _{p}}\) is x × 10−1. The value of x is:
(Rounded off to the nearest integer)
(Mass of Li3+ = 8.3 the mass of a proton)
1. 4
2. 6
3. 2
4. 8
The quantum number of four electrons are given below :
| I. | n = 4, l=2 , ml = -2, ms = \(-\frac{1}{2}\) |
| II. | n=3, l=2, ml = 1, ms = \(+\frac{1}{2}\) |
| III. | n=4 , l=1, ml = 0, ms = \(+\frac{1}{2}\) |
| IV. | n=3, l=1, ml=1, ms=\(-\frac{1}{2}\) |
The correct order of their increasing energies will be:
1. I < III < II < IV
2. IV < II < III < I
3. I < II < III < IV
4. IV < III < II < I
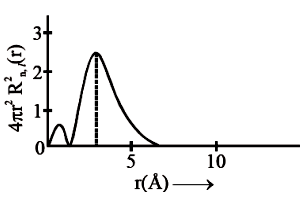
The graph between and r (radial distance) is shown below. This represents:
1. 3s orbital
2. 2s orbital
3. 2p orbital
4. 1s orbital
The radius of the second Bohr orbit for hydrogen atom is:
(Planck's Const. h = 6.6262 × 10–34 Js; mass of electron = 9.1091 × 10–31 kg; charge of electron e = 1.60210 ×10–19 C; permittivity of vaccum ∈0 = 8.854185 ×10–12 kg–1m–3A2)
1. 0.529 Å
2. 2.12 Å
3. 1.65 Å
4. 7.76 Å
The correct set of four quantum numbers for the valence electrons of rubidium atom (Z = 37) is -
1. 5, 1, 0 +
2. 5, 1, 1 +
3. 5, 0, 1 +
4. 5, 0, 0 +
© 2025 GoodEd Technologies Pvt. Ltd.