- 1(current)
Q. No.The set of a quantum number that represents degenerate orbitals is:
1. a
2. b
3. c
4. a, b
| a. | \( \small{n=3, \ell=2, m=0, s=\frac{-1}{2} \,\& \ \,n=3, \ell=2, m=-1, s=\frac{+1}{2}}\) |
| b. | \(\small{n=2, \ell=1, m=1 , \ s=\frac{-1}{2}\, \&\, \ n=3, \ell=1, m=1 \mathrm{~s}=\frac{+1}{2}}\) |
| c. | \(\small{n=4, \ell=2, m=-1, s=\frac{1}{2}\, \&\, \ n=3, \ell=2, m=-1, s=\frac{1}{2}}\) |
1. a
2. b
3. c
4. a, b
Subtopic: Quantum Numbers & Schrodinger Wave Equation |
71%
From NCERT
JEE
Please attempt this question first.
Hints
Please attempt this question first.
Using the following statements, identify the correct set of statements:
1. (i), (ii), (iii)
2. (i), (ii), (iv)
3. (i), (ii), (iii), (iv)
4. (i), (iii), (iv)
| (i). | n (principal quantum number) can have values 1, 2, 3, 4, ....... |
| (ii). | The number of orbitals for a given value of l is (2l+1). |
| (iii). | The value of spin quantum numbers is always \(\pm\frac12\). |
| (iv). | For l=5, the total number of orbitals is 9. |
1. (i), (ii), (iii)
2. (i), (ii), (iv)
3. (i), (ii), (iii), (iv)
4. (i), (iii), (iv)
Subtopic: Quantum Numbers & Schrodinger Wave Equation |
85%
From NCERT
JEE
Please attempt this question first.
Hints
Please attempt this question first.
The plots of radial distribution functions for various orbitals of hydrogen atom against 'r' are given below:
a.
b.
c.
d.
The correct plot for 3s orbital is:
1. (B)
2. (A)
3. (D)
4. (C)
Subtopic: Quantum Numbers & Schrodinger Wave Equation |
JEE
Please attempt this question first.
Hints
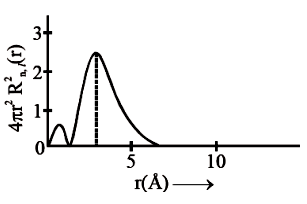
The graph between and r (radial distance) is shown below. This represents:
| 1. | 3s orbital | 2. | 2s orbital |
| 3. | 2p orbital | 4. | 1s orbital |
Subtopic: Quantum Numbers & Schrodinger Wave Equation |
63%
From NCERT
Please attempt this question first.
Hints
Please attempt this question first.
The correct set of four quantum numbers for the valence electrons of rubidium atom (Z = 37) is -
1. 5, 1, 0 +
2. 5, 1, 1 +
3. 5, 0, 1 +
4. 5, 0, 0 +
Subtopic: Quantum Numbers & Schrodinger Wave Equation |
84%
From NCERT
JEE
Please attempt this question first.
Hints
Please attempt this question first.
Consider the ground state of Cr atom (Z=24). The numbers of electrons with the azimuthal quantum numbers, l=1 and 2 are, respectively:
1. 12 and 4
2. 12 and 5
3. 16 and 4
4. 16 and 5
Subtopic: Quantum Numbers & Schrodinger Wave Equation |
76%
From NCERT
JEE
Please attempt this question first.
Hints
Please attempt this question first.
How many sets of quantum numbers are possible?
1. 0
2. 1
3. 2
4. 3
| n | l | m | |
| (a). | 2 | 2 | 1 |
| (b). | 3 | 2 | -2 |
| (c). | 3 | 2 | -1 |
| (d). | 2 | 1 | -1 |
1. 0
2. 1
3. 2
4. 3
Subtopic: Quantum Numbers & Schrodinger Wave Equation |
87%
From NCERT
JEE
Please attempt this question first.
Hints
Please attempt this question first.
- 1(current)
Q. No.
© 2025 GoodEd Technologies Pvt. Ltd.