Select Chapter Topics:
Q. No.\(n\) moles of a perfect gas undergoes a cyclic process ABCA (see figure) consisting of the following processes.
| \(A\rightarrow B\) | Isothermal expansion at temperature \(T\) so that the volume is doubled from \(V_1\) to \(V_2=2V_1\) and pressure changes from \(P_1\) to \(P_2.\) |
| \(B\rightarrow C\) | Isobaric compression at pressure \(P_2\) to initial volume \(V_1\). |
| \(C\rightarrow A\) | Isochoric change leading to change of pressure from \(P_2\) to \(P_1\). |
Total work done in the complete cycle \(ABCA\) is:
1. \(0\)
2. \(nRT(\ln 2-\frac{1}{2})\)
3. \(nRT\ln 2\)
4. \(nRT(\ln 2+\frac{1}{2})\)
Subtopic: Work Done by a Gas |
From NCERT
Please attempt this question first.
Hints
Please attempt this question first.
The same amount of heat is supplied to equimolar masses of hydrogen and helium, under constant pressure. The work done by the two gases, \(H_2\) and \(He,\) are \(W_1\) and \(W_2.\) Then:
| 1. | \(W_1>W_2\) |
| 2. | \(W_1<W_2\) |
| 3. | \(W_1=W_2\) |
| 4. | \(W_1\) and \(W_2\) cannot be compared unless the temperatures are known. |
Subtopic: Work Done by a Gas |
From NCERT
To view explanation, please take trial in the course.
NEET 2026 - Target Batch
Hints
To view explanation, please take trial in the course.
NEET 2026 - Target Batch
A monoatomic ideal gas undergoes a process given by the equation: \({\dfrac{pT}{V}}=\text{constant.}\) The molar specific heat capacity in the process equals:
| 1. | \({\dfrac{3}{2}}R\) | 2. | \({\dfrac{5}{2}}R\) |
| 3. | \({\dfrac{1}{2}}R\) | 4. | zero |
Subtopic: Molar Specific Heat |
From NCERT
To view explanation, please take trial in the course.
NEET 2026 - Target Batch
Hints
To view explanation, please take trial in the course.
NEET 2026 - Target Batch
The quantity of heat required to take a system from \(\mathrm{A}\) to \(\mathrm{C}\) through the process \(\mathrm{ABC}\) is \(20\) cal. The quantity of heat required to go from \(\mathrm{A}\) to \(\mathrm{C}\) directly is:
1. \(20\) cal
2. \(24.2\) cal
3. \(21\) cal
4. \(23\) cal
Subtopic: Cyclic Process |
From NCERT
To view explanation, please take trial in the course.
NEET 2026 - Target Batch
Hints
To view explanation, please take trial in the course.
NEET 2026 - Target Batch
A Carnot engine has an efficiency of \(50\%\). If the temperature of sink is reduced by \(40^{\circ}\text{C}\), its efficiency increases by \(30\%\). The temperature of the source will be:
1. \(166.7\) K
2. \(255.1\) K
3. \(266.7\) K
4. \(367.7\) K
1. \(166.7\) K
2. \(255.1\) K
3. \(266.7\) K
4. \(367.7\) K
Subtopic: Carnot Engine |
From NCERT
Please attempt this question first.
Hints
Please attempt this question first.
An ideal monoatomic gas at a temperature of \(300\) K and a pressure of \(10\) atm is suddenly allowed to expand into vacuum so that its volume is doubled. No exchange of heat is allowed to take place between the gas and its surroundings during the process. After equilibrium is reached, the final temperature is:
| 1. | \(300\) K | 2. | \(\dfrac{300}{2^{5/3}}\) K |
| 3. | \(\dfrac{300}{2^{2/3}}\) K | 4. | \(600\) K |
Subtopic: Types of Processes |
From NCERT
To view explanation, please take trial in the course.
NEET 2026 - Target Batch
Hints
To view explanation, please take trial in the course.
NEET 2026 - Target Batch
Two monoatomic gases \(A,B\) are taken in two parts of a vessel having equal volumes \(V_0.\) The gases are at the same pressure \(P_0\) but at temperature of \(300~\text K\) and \(600~\text K.\) There is a partition between the parts of the vessel. The partition is removed, and the gases are allowed to mix. The vessel, as a whole, is insulated. The final temperature of the system is:
1. \(450~\text K\)
2. \(400~\text K\)
3. \(500~\text K\)
4. \(550~\text K\)
1. \(450~\text K\)
2. \(400~\text K\)
3. \(500~\text K\)
4. \(550~\text K\)
Subtopic: Work Done by a Gas |
From NCERT
To view explanation, please take trial in the course.
NEET 2026 - Target Batch
Hints
To view explanation, please take trial in the course.
NEET 2026 - Target Batch
In \(1^{\text{st}}\) case, Carnot engine operates between temperatures \(300\) K and \(100\) K. In \(2^{\text{nd}}\) case, as shown in the figure, a combination of two engines is used. The efficiency of this combination (in \(2^{\text{nd}}\) case) will be:
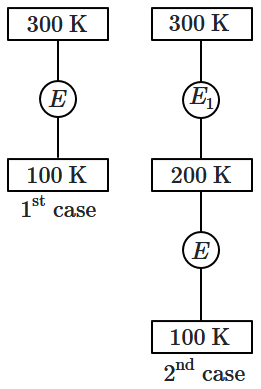
| 1. | same as the \(1^{\text{st}}\) case. |
| 2. | always greater than the \(1^{\text{st}}\) case. |
| 3. | always less than the \(1^{\text{st}}\) case. |
| 4. | may increase or decrease with respect to the \(1^{\text{st}}\) case. |
Subtopic: Carnot Engine |
From NCERT
Please attempt this question first.
Hints
Please attempt this question first.
A monoatomic gas \((A)\) and a diatomic gas \((B)\) are taken in two separate identical containers at the same conditions of temperature and pressure.
The two gases \(A,B\) are allowed to expand adiabatically until their volumes are doubled. The final temperatures are \(\theta_A\) (for gas \(A\)) and \(\theta_B\) (for gas \(B\)). Then:
The two gases \(A,B\) are allowed to expand adiabatically until their volumes are doubled. The final temperatures are \(\theta_A\) (for gas \(A\)) and \(\theta_B\) (for gas \(B\)). Then:
| 1. | \(\theta_A=\theta_B\) |
| 2. | \(\theta_A<\theta_B\) |
| 3. | \(\theta_A>\theta_B\) |
| 4. | the relationship between \(\theta_A,\theta_B\) depends on the molecular weights of \(A\) and \(B\) |
Subtopic: Types of Processes |
From NCERT
To view explanation, please take trial in the course.
NEET 2026 - Target Batch
Hints
To view explanation, please take trial in the course.
NEET 2026 - Target Batch
An ideal gas forms the working substance of a Carnot engine, and is taken around the Carnot cycle. We form the integral: \(I=\int\dfrac{dQ}{T},\)
where \(dQ\) is the heat supplied to the gas and \(T\) is the temperature of the gas. The integral is evaluated over the entire cycle. The value of the integral \(I\) is:
where \(dQ\) is the heat supplied to the gas and \(T\) is the temperature of the gas. The integral is evaluated over the entire cycle. The value of the integral \(I\) is:
| 1. | zero |
| 2. | negative |
| 3. | positive |
| 4. | non-negative(positive or zero) |
Subtopic: Carnot Engine |
From NCERT
To view explanation, please take trial in the course.
NEET 2026 - Target Batch
Hints
To view explanation, please take trial in the course.
NEET 2026 - Target Batch
Select Chapter Topics:
© 2025 GoodEd Technologies Pvt. Ltd.