A particle of mass \(m\) moving in the \(x\) direction with speed \(2v\) is hit by another particle of mass \(2m\) moving in the \(y\) direction with speed \(v\). If the collision is perfectly inelastic, the percentage loss in the energy during the collision is close to:
1. \(44\%\)
2. \(50\%\)
3. \(56\%\)
4. \(62\%\)

1. \({mv^2\over 2(L-nr)}\)
2. \({mv^2\over L-2nr}\)
3. \({mv^2\over L-nr}\)
4. zero

1. \(\tan\theta=\dfrac{\sqrt3+\sqrt2}{1-\sqrt2} \)
2. \(\tan\theta=\dfrac{1-\sqrt3}{1+\sqrt2}\)
3. \(\tan\theta=\dfrac{\sqrt3-\sqrt2}{1-\sqrt2}\)
4. \(\tan\theta=\dfrac{1-\sqrt3}{\sqrt2(1+\sqrt3)}\)
In a collinear collision, a particle with an initial speed \(v_0\) strikes a stationary particle of the same mass. If the final total kinetic energy is \(50\%\) greater than the original kinetic energy, the magnitude of the relative velocity between the two particles, after collision, is:
1. \(\frac{{v_0}}{4}\)
2. \(\sqrt{2}{v_0}\)
3. \(\frac{{v_0}}{2}\)
4. \(\frac{{v_0}}{\sqrt{2}}\)
It is found that if a neutron suffers an elastic collinear collision with deuterium at rest, fractional loss of its energy is \(P_d\); while for its similar collision with carbon nucleus at rest, fractional loss of energy is \(P_c\). The values of \(P_d\) and \(P_c\) are respectively:
1. \(0.89,~0.28\)
2. \(0.28, ~0.89\)
3. \(0,~0\)
4. \(0,~1\)
A body of mass \(m_1\) moving with an unknown velocity of \(v_1 \hat{i},\), undergoes a collinear collision with a body of mass \(m_2\) moving with a velocity \(v_2\hat{i}.\). After collision, \(m_1\) and \(m_2\) move with velocities of \(v_3\hat{i}\) and \(v_4\hat{i},\) respectively . If \(m_2=0.5m_1\) and \(v_3=0.5v_1\), then \(v_1\) is:
1. \( v_4-\frac{v_2}{4} \)
2. \( v_4+v_2 \)
3. \( v_4-\frac{v_2}{2} \)
4. \( v_4-v_2\)
A body of mass \(2~\text{kg}\) makes an elastic collision with a second body at rest and continues to move in the original direction but with one fourth of its original speed. What is the mass of the second body?
1. \(1.5~\text{kg}\)
2. \(1.2~\text{kg}\)
3. \(1.0~\text{kg}\)
4. \(1.8~\text{kg}\)
| 1. | \(\sqrt{2}v\) | 2. | \(\dfrac{v}{2\sqrt{2}}\) |
| 3. | \(\dfrac{v}{\sqrt{2}}\) | 4. | \(2\sqrt{2}v\) |
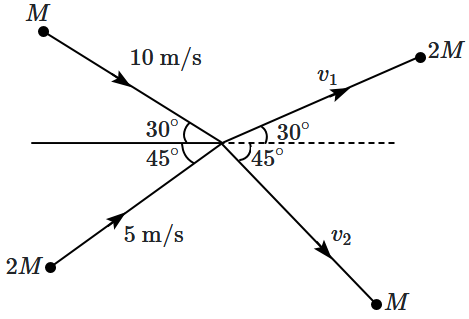
Two particles, of masses \(M\) and \(2M\), moving, as shown, with speeds of \(10~\text{m/s}\) and \(5~\text{m/s}\), collide elastically at the origin. After the collision, they move along the indicated directions with speeds \(v_1\) and \(v_2\), respectively. The values of \(v_1\) and \(v_2\) are nearly:
| 1. | \(3.2~\text{m/s}~\text{and}~12.6~\text{m/s}\) |
| 2. | \(3.2~\text{m/s}~\text{and}~6.3~\text{m/s}\) |
| 3. | \(6.5~\text{m/s}~\text{and}~6.3~\text{m/s}\) |
| 4. | \(6.5~\text{m/s}~\text{and}~3.2~\text{m/s}\) |

1. \(5\)
2. \(2\)
3. \(4\)
4. \(3\)