In an \(\text{AC}\) circuit, the power dissipated in a resistance is found to \(P_1\) when a source voltage of \(V_1\) is connected across it. If the same resistance is connected in series with a capacitance and the same source is connected across the combination, the power in the resistance is found to be \(P_2=\dfrac{P_1}{2}.\) The phase difference between the voltage and the current is:
1. \(30^{\circ}\)
2. \(60^{\circ}\)
3. \(45^{\circ}\)
4. \(90^{\circ}\)
1. \(30^{\circ}\)
2. \(60^{\circ}\)
3. \(45^{\circ}\)
4. \(90^{\circ}\)
Subtopic: Different Types of AC Circuits |
From NCERT
To view explanation, please take trial in the course.
NEET 2026 - Target Batch - Vital
Hints
To view explanation, please take trial in the course.
NEET 2026 - Target Batch - Vital
An alternating \(\text{emf}= V_0\sin \omega t\) is applied between the two ends \(A\) & \(B\) of the circuit shown below. The current through \(C\) has the same RMS value as that through \(R.\) The RMS value of the current flowing out at \(B\) is:

1. \(\dfrac{V_0}{ \sqrt 2 R}\)
2. \(\dfrac{V_0}{ R}\)
3. \(\dfrac{ \sqrt 2 V_0}{R}\)
4. zero

1. \(\dfrac{V_0}{ \sqrt 2 R}\)
2. \(\dfrac{V_0}{ R}\)
3. \(\dfrac{ \sqrt 2 V_0}{R}\)
4. zero
Subtopic: Different Types of AC Circuits |
From NCERT
Please attempt this question first.
Hints
An alternating current generator has an internal resistance \(R_{g}\) and an internal reactance \(X_{g}\). It is used to supply power to a passive load consisting of a resistance \(R_{g}\) and a reactance \(X_{L}\). For maximum power to be delivered from the generator to the load, the value of \(X_{L}\) is equal to:
1. zero
2. \(X_g\)
3. \(-X_g\)
4. \(R_g\)
Subtopic: Different Types of AC Circuits |
From NCERT
To view explanation, please take trial in the course.
NEET 2026 - Target Batch - Vital
Hints
To view explanation, please take trial in the course.
NEET 2026 - Target Batch - Vital
Given below are two statements: one is labelled as Assertion (A) and the other is labelled as Reason (R):
| Assertion (A): | On the increasing frequency of a.c. through a conductor resistance of the circuit may increase. |
| Reason (R): | Resistance of a conductor is directly proportional to the frequency of the a.c. input. |
In the light of the above statements choose the correct answer from the options given below:
| 1. | Both (A) and (R) are true and (R) is the correct explanation of (A). |
| 2. | Both (A) and (R) are true but (R) is not the correct explanation of (A). |
| 3. | (A) is true but (R) is false. |
| 4. | Both (A) and (R) are false. |
Subtopic: Different Types of AC Circuits |
From NCERT
To view explanation, please take trial in the course.
NEET 2026 - Target Batch - Vital
Hints
To view explanation, please take trial in the course.
NEET 2026 - Target Batch - Vital
An \(RC\) circuit is connected to a \(10\) V AC source and it is observed to supply a \(200\) mA current at a frequency of \(100\) kHz. The same resistance is now paired with an inductor \((L)\) in series and the same source supplies \(200\) mA current at a frequency of \(1\) kHz at the same operating voltage. If the circuit were made with the given \(L\text-C\text-R\) in series, the current will be a maximum when the frequency is \(f_o\). Then,
| 1. | \(f_o = \dfrac{10^3 + 10^5}{2}\) Hz |
| 2. | \(f_o > \dfrac{10^3 + 10^5}{2}\) Hz |
| 3. | \(f_o < \dfrac{10^3 + 10^5}{2}\) Hz |
| 4. | \(f_o = {10^3 + 10^5}\) Hz |
Subtopic: Different Types of AC Circuits |
From NCERT
To view explanation, please take trial in the course.
NEET 2026 - Target Batch - Vital
Hints
To view explanation, please take trial in the course.
NEET 2026 - Target Batch - Vital
The RMS voltage across the inductor is twice that across the capacitor, while the applied RMS voltage across the entire combination (i.e. \(V_{AX}\)) is \(V_r\). The RMS voltage across the capacitor is:


| 1. | \(\dfrac{V_r}{3}\) | 2. | \(\dfrac{2V_r}{3}\) |
| 3. | \(\dfrac{V_r}{2}\) | 4. | \(V_r\) |
Subtopic: Different Types of AC Circuits |
From NCERT
To view explanation, please take trial in the course.
NEET 2026 - Target Batch - Vital
Hints
To view explanation, please take trial in the course.
NEET 2026 - Target Batch - Vital
Given below are two statements:
| Assertion (A): | A capacitor can replace the choke coils in an AC circuit. |
| Reason (R): | A capacitor can reduce the current in an AC circuit like an inductor |
In the light of the above statements choose the correct answer from the options given below:
| 1. | Both (A) and (R) are true and (R) is the correct explanation of (A). |
| 2. | Both (A) and (R) are true but (R) is not the correct explanation of (A). |
| 3. | (A) is true but (R) is false. |
| 4. | Both (A) and (R) are false. |
Subtopic: Different Types of AC Circuits |
From NCERT
To view explanation, please take trial in the course.
NEET 2026 - Target Batch - Vital
Hints
To view explanation, please take trial in the course.
NEET 2026 - Target Batch - Vital
When an AC voltage of \(220\) V is applied to the capacitor \(C\)
Choose the correct options:
| (a) | the maximum voltage between plates is \(220\) V. |
| (b) | the current is in phase with the applied voltage. |
| (c) | the charge on the plates is in phase with the applied voltage. |
| (d) | power delivered to the capacitor is zero. |
| 1. | (b), (c) | 2. | (a), (d) |
| 3. | (b), (d) | 4. | (c), (d) |
Subtopic: Different Types of AC Circuits |
From NCERT
To view explanation, please take trial in the course.
NEET 2026 - Target Batch - Vital
Hints
To view explanation, please take trial in the course.
NEET 2026 - Target Batch - Vital
Sinusoidal voltages are applied at \(X\) and \(Y\) so that the currents flowing into the capacitor at \(X\) and into the resistor at \(Y\) are equal and out of phase with each other. The RMS values of the voltages across the capacitor and the resistor are each equal to \(V_r\). The RMS value of \(V_X-V_Y\) is:
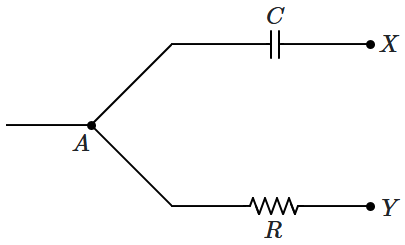

| 1. | zero | 2. | \(\sqrt 2 V_r \) |
| 3. | \(2 V_r\) | 4. | \(\dfrac{V_r}{\sqrt 2}\) |
Subtopic: Different Types of AC Circuits |
From NCERT
To view explanation, please take trial in the course.
NEET 2026 - Target Batch - Vital
Hints
To view explanation, please take trial in the course.
NEET 2026 - Target Batch - Vital
In an \(LCR\) series circuit, the potential difference across each element is initially \(60~\text V.\) Now the value of resistance alone is doubled, then the potential drops across \(R,\) \(L\) and \(C\), respectively are:
| 1. | \(60~\text{V},~30~\text{V},~30~\text{V}\) |
| 2. | \(60~\text{V},~120~\text{V},~120~\text{V}\) |
| 3. | \(30~\text{V},~120~\text{V},~120~\text{V}\) |
| 4. | \(60~\text{V},~100~\text{V},~80~\text{V}\) |
Subtopic: Different Types of AC Circuits |
54%
Please attempt this question first.
Hints
Please attempt this question first.




