A straight wire of mass \(200~\text{g}\) and length \(1.5~\text{m}\) carries a current of \(2~\text{A}.\) It is suspended in mid-air by a uniform horizontal magnetic field \(B\) (shown in the figure). What is the magnitude of the magnetic field?

| 1. | \(0.65~\text{T}\) | 2. | \(0.77~\text{T}\) |
| 3. | \(0.44~\text{T}\) | 4. | \(0.20~\text{T}\) |
In a region of space, magnetic field is parallel to the positive \(y\text-\)axis and the charged particle is moving along the positive \(x\text-\)axis (as shown in the figure). The directions of Lorentz force for an electron (negative charge) and proton (positive charge) are respectively:

| 1. | \(-z\text-\)axis, \(+z\text-\)axis | 2. | \(+z\text-\)axis, \(-z\text-\)axis |
| 3. | \(-z\text-\)axis, \(-z\text-\)axis | 4. | \(+z\text-\)axis, \(+z\text-\)axis |
The radius of the path of an electron and frequency (mass and charge ) moving at a speed of \(3\times10^7\) m/s in a magnetic field of \(6\times10^{-4}\) T perpendicular to it are respectively:
1. \(24\) cm, \(4\) MHz
2. \(22\) cm, \(4\) MHz
3. \(28\) cm, \(2\) MHz
4. \(26\) cm, \(2\) MHz
An electron is moving at a speed of 3 ×107 m/s in a magnetic field perpendicular to it. The energy of the electron in keV is: ( 1 eV = 1.6 × 10–19 J)
1. 2.5 keV
2. 3.5 keV
3. 20 keV
4. 3.0 keV
An element \(\Delta l=\Delta x \hat{i}\) is placed at the origin and carries a large current of \(I=10~\text A\) (as shown in the figure). What is the magnetic field on the \(y\text-\)axis at a distance of \(0.5~\text m?\)
\((\text{Given}~\Delta x=1~\text{cm})\)

| 1. | \(6\times 10^{-8}~\text{T}\) | 2. | \(4\times 10^{-8}~\text{T}\) |
| 3. | \(5\times 10^{-8}~\text{T}\) | 4. | \(5.4\times 10^{-8}~\text{T}\) |
| 1. | \(0\) | 2. | \(1.2\times 10^{-4}~\text{T}\) |
| 3. | \(2.1\times 10^{-4}~\text{T}\) | 4. | None of these |
A straight wire carrying a current of \(12~\text A\) is bent into a semi-circular arc of radius \(2.0 ~\text{cm}\) as shown in the figure. Consider the magnetic field \(B\) at the centre of the arc. What is the magnetic field at centre due to the semi-circular loop?

1. Zero
2. \( 3 . 8 \times10^{- 4} ~\text T\)
3. \(1.9\times10^{- 4} ~\text T\)
4. \(2.9 \times10^{- 4} ~\text T\)
Consider a tightly wound \(100\) turn coil of radius \(10\) cm, carrying a current of \(1\) A. What is the magnitude of the magnetic field at the centre of the coil?
| 1. | \(8.2\times10^{-4}\) T | 2. | \(4.6\times10^{-4}\) T |
| 3. | \(5.2\times10^{-4}\) T | 4. | \(6.2\times10^{-4}\) T |
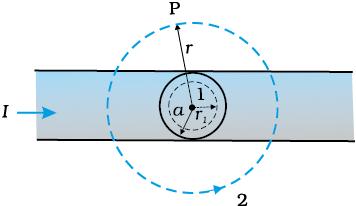
The figure shows a long straight wire of a circular cross-section (radius a) carrying steady current I. The current I is uniformly distributed across this cross-section. If the magnetic field in the region (r < a) is and for (r > a) is , then is:
A solenoid of length \(0.5~\text m\) has a radius of \(1~\text{cm}\) and is made up of \(500\) turns. It carries a current of \(5~\text A.\) What is the magnitude of the magnetic field inside the solenoid?
1. \(6.28\times 10^{-3}~\text T\)
2. \(3.14\times 10^{-3}~\text T\)
3. \(2.72\times 10^{-3}~\text T\)
4. \(5.17\times 10^{-3}~\text T\)







