- 1(current)
Q. No.A ball with a mass of \(100\) g is dropped from a height of \(h=10\) cm onto a platform fixed at the top of a vertical spring (as shown in the figure). The ball remains on the platform, and the platform is depressed by a distance of \(\dfrac {h} {2}.\) The spring constant is: (use \(g=10\) ms-2)
| 1. | \(100\) Nm–1 | 2. | \(110\) Nm–1 |
| 3. | \(120\) Nm–1 | 4. | \(130\) Nm–1 |
Subtopic: Elastic Potential Energy |
75%
From NCERT
JEE
Please attempt this question first.
Hints
Please attempt this question first.
As per the given figure, two blocks each of mass \(250 ~\text{g}\) are connected to a spring of spring constant \(2~\mathrm{Nm^{-1}}.\) If both are given velocity \(v\) in opposite directions, then the maximum elongation of the spring is:
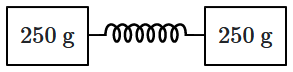
| 1. | \(\dfrac{v } {2 \sqrt 2}\) | 2. | \(\dfrac{v } {2}\) |
| 3. | \(\dfrac{v } {4}\) | 4. | \(\dfrac{v } { \sqrt 2}\) |
Subtopic: Elastic Potential Energy |
51%
From NCERT
JEE
Please attempt this question first.
Hints
Please attempt this question first.
A block of mass \(m\) (as shown in the figure) moving with kinetic energy \(E\) compresses a spring through a distance \(25~\text{cm}\) when, its speed is halved. The value of the spring constant of the used spring is \(nE~\text{Nm}^{-1}.\) The value of \(n\) will be:
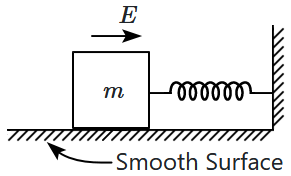
1. \(32\)
2. \(24\)
3. \(20\)
4. \(16\)
1. \(32\)
2. \(24\)
3. \(20\)
4. \(16\)
Subtopic: Elastic Potential Energy |
54%
From NCERT
JEE
Please attempt this question first.
Hints
Please attempt this question first.
At equilibrium position, a \(75\) N force starts is acting on the block attached with the spring as shown in the figure. Maximum extension in the spring is:
1. \(1\) m
2. \(3\) m
3. \(4\) m
4. \(2\) m
1. \(1\) m
2. \(3\) m
3. \(4\) m
4. \(2\) m
Subtopic: Elastic Potential Energy |
From NCERT
JEE
Please attempt this question first.
Hints
Please attempt this question first.
- 1(current)
Q. No.
© 2025 GoodEd Technologies Pvt. Ltd.