The figure given below depicts two circular motions. The radius of the circle, the period of revolution, the initial position, and the sense of revolution are indicated in the figures.  Equations of the \(x\)-projection of the radius vector of the rotating particle \(\mathrm P\) in each case are, respectively:

 
 

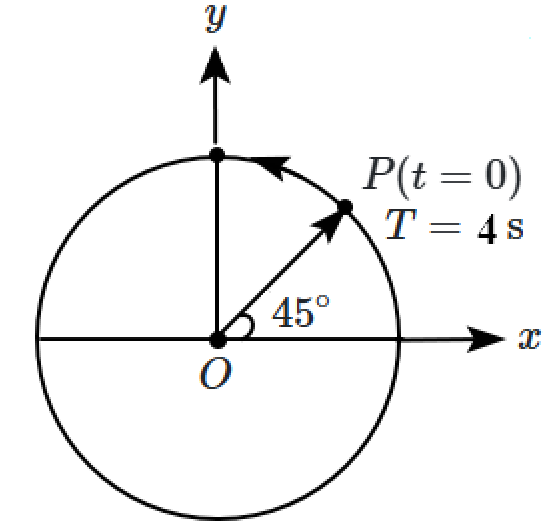
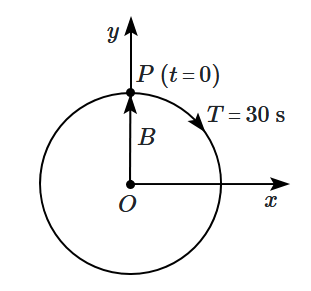
1.	\(\small{x}({t})={A} \cos \left(\dfrac{2 \pi}{4} {t}+\dfrac{\pi}{4}\right)\text{ and }{x}({t})={B} \cos \left(\dfrac{\pi}{15} {t}-\dfrac{\pi}{2}\right)\)
2.	\(\small{x}({t})={A} \cos \left(\dfrac{2 \pi}{4} {t}+\dfrac{\pi}{4}\right)\text{ and }{x}({t})={B} \sin \left(\dfrac{\pi}{15} {t}-\dfrac{\pi}{2}\right)\)
3.	\(\small{x}({t})={A} \cos \left(\dfrac{2 \pi}{4} {t}+\dfrac{\pi}{4}\right)\text{ and }{x}({t})={B} \cos \left(\dfrac{\pi}{15} {t}-\dfrac{\pi}{4}\right)\)
4.	\(\small{x}({t})={A} \sin \left(\dfrac{2 \pi}{4} {t}+\dfrac{\pi}{4}\right)\text{ and }{x}({t})={B} \cos \left(\dfrac{\pi}{15} {t}-\dfrac{\pi}{2}\right)\)