- 1(current)
Q. No.Water from a tap emerges vertically downwards with an initial speed of \(1.0~\text{m/s}\). The cross-sectional area of the tap is \(10^{-4}~\text{m}^2\). Assume that the pressure is constant throughout the stream of water and that the flow is streamlined. The cross-sectional area of the stream, \(0.15~\text{m}\) below the tap would be: (take \(g=10~\text{m/s}^2\))
1. \(5\times10^{-4}~\text{m}^2\)
2. \(2\times10^{-5}~\text{m}^2\)
3. \(5\times10^{-5}~\text{m}^2\)
4. \(1\times10^{-5}~\text{m}^2\)
Subtopic: Bernoulli's Theorem |
81%
Level 1: 80%+
Please attempt this question first.
Hints
Please attempt this question first.
A fluid is flowing through a horizontal pipe of varying cross-sections, with speed \(v\) ms-1 at a point where the pressure is \(P\) pascal. At another point where pressure is \(\dfrac{P}{2}\) pascal, its speed is \(V\) ms-1. If the density of the fluid is \(\rho\) kg-m-3 and the flow is streamlined, then \(V\) is equal to:
| 1. | \(\sqrt{\dfrac{P}{2\rho }+v^{2}}\) | 2. | \(\sqrt{\dfrac{P}{\rho }+v^{2}} \) |
| 3. | \(\sqrt{\dfrac{2P}{\rho }+v^{2}}\) | 4. | \(\sqrt{\dfrac{P}{\rho }+v^{}}\) |
Subtopic: Bernoulli's Theorem |
72%
Level 2: 60%+
Please attempt this question first.
Hints
Please attempt this question first.
An ideal fluid with a density of \(800\) \(\text{kg}/\text{m}^3\) flows smoothly through a bent pipe that gradually narrows. The pipe's cross-sectional area decreases from \(a\) at the entrance to \(\dfrac{a}{2}\) at the exit. The pressure at the wider section exceeds the pressure at the narrower section by \(4100\) Pa. Given that the fluid velocity at the wider section is \(\dfrac{\sqrt x}{6}~\text{m}/\text{s}\) and the vertical height difference between the two sections is \(1~\text{m},\) then the value of \(x\) is: (use \(g=10~\text{m}/\text{s}^2\))
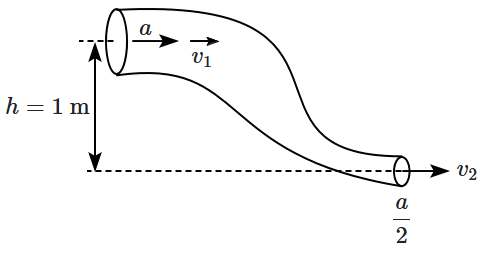
1. \(124\)
2. \(236\)
3. \(363\)
4. \(432\)
1. \(124\)
2. \(236\)
3. \(363\)
4. \(432\)
Subtopic: Bernoulli's Theorem |
69%
Level 2: 60%+
Please attempt this question first.
Hints
Please attempt this question first.
The area of the cross-section of a large tank is \(0.5~\text{m}^2\). It has a narrow opening near the bottom having an area of cross-section \(1~\text{cm}^2\). A load of \(25~\text{kg}\) is applied on the water at the top of the tank. Neglecting the speed of water in the tank, the velocity of the water, coming out of the opening at the time when the height of the water level in the tank is \(40~\text{cm}\) above the bottom, will be: [Take \(g = 10~\text{ms}^{-2}\)]
1. \(1~\text{ms}^{-1}\)
2. \(2~\text{ms}^{-1}\)
3. \(3~\text{ms}^{-1}\)
4. \(4~\text{ms}^{-1}\)
1. \(1~\text{ms}^{-1}\)
2. \(2~\text{ms}^{-1}\)
3. \(3~\text{ms}^{-1}\)
4. \(4~\text{ms}^{-1}\)
Subtopic: Bernoulli's Theorem |
70%
Level 2: 60%+
JEE
Please attempt this question first.
Hints
Please attempt this question first.
A liquid of density \(750~\text{kgm}^{-3}\) flows smoothly through a horizontal pipe that tapers in cross-sectional area from \(A_1 = 1.2 \times 10^{-2}~\text{m}^2\) to \(A_2 = \frac{A_1}{2}\). The pressure difference between the wide and narrow sections of the pipe is \(4500~\text{Pa}\). The rate of flow of liquid is:
1. \(20\times 10^{-3}~\text{m}^{-3}\text{s}^{-1}\)
2. \(30\times 10^{-3}~\text{m}^{-3}\text{s}^{-1}\)
3. \(28\times 10^{-3}~\text{m}^{-3}\text{s}^{-1}\)
4. \(24\times 10^{-3}~\text{m}^{-3}\text{s}^{-1}\)
1. \(20\times 10^{-3}~\text{m}^{-3}\text{s}^{-1}\)
2. \(30\times 10^{-3}~\text{m}^{-3}\text{s}^{-1}\)
3. \(28\times 10^{-3}~\text{m}^{-3}\text{s}^{-1}\)
4. \(24\times 10^{-3}~\text{m}^{-3}\text{s}^{-1}\)
Subtopic: Bernoulli's Theorem |
79%
Level 2: 60%+
JEE
Please attempt this question first.
Hints
Please attempt this question first.
Water is flowing inside the conical type tube having a ratio of area of cross-section \(6:1\). If the speed of the water outlet through a smaller area is \(60~\text{m/s}\), then the pressure difference across these two cross-sections is:
(assume incompressible fluid, density of water = \(1000~\text{kg/m}^3\) )
1. \(175\times 10^4~ \text{Pa}\)
2. \(175\times 10^3~ \text{Pa}\)
3. \(250\times 10^4~ \text{Pa}\)
4. \(250\times 10^3~ \text{Pa}\)
(assume incompressible fluid, density of water = \(1000~\text{kg/m}^3\) )
1. \(175\times 10^4~ \text{Pa}\)
2. \(175\times 10^3~ \text{Pa}\)
3. \(250\times 10^4~ \text{Pa}\)
4. \(250\times 10^3~ \text{Pa}\)
Subtopic: Bernoulli's Theorem |
74%
Level 2: 60%+
JEE
Please attempt this question first.
Hints
Please attempt this question first.
The pressures at the ends of a horizontal pipe are given for water. The speed \({v}\) at end \(2\) if the speed at end \(1\) is \(10~\text{m/s}.\) (density of water \(=1000~\text{kg/m}^3\)). Then the speed \({v}\) (in \(\text{m/s}\)) is:
1. \(22\)
2. \(33\)
3. \(11\)
4. \(55\)
1. \(22\)
2. \(33\)
3. \(11\)
4. \(55\)
Subtopic: Bernoulli's Theorem |
83%
Level 1: 80%+
JEE
Please attempt this question first.
Hints
Please attempt this question first.
Correct Bernoulli's equation is (symbols have their usual meaning) :
1. \(P+\rho g h+\frac{1}{2} \rho v^2=\text { constant }\)
2. \(\mathrm{P}+\rho \mathrm{gh}+\rho \mathrm{v}^2=\mathrm{constant}\)
3. \(P+\mathrm{mgh}+\frac{1}{2} \mathrm{mv}^2=\text { constant }\)
4. \(\mathrm{P}+\frac{1}{2} \rho g h+\frac{1}{2} \rho \mathrm{v}^2=\text { constant }\)
1. \(P+\rho g h+\frac{1}{2} \rho v^2=\text { constant }\)
2. \(\mathrm{P}+\rho \mathrm{gh}+\rho \mathrm{v}^2=\mathrm{constant}\)
3. \(P+\mathrm{mgh}+\frac{1}{2} \mathrm{mv}^2=\text { constant }\)
4. \(\mathrm{P}+\frac{1}{2} \rho g h+\frac{1}{2} \rho \mathrm{v}^2=\text { constant }\)
Subtopic: Bernoulli's Theorem |
95%
Level 1: 80%+
Please attempt this question first.
Hints
Please attempt this question first.
- 1(current)
Q. No.
© 2025 GoodEd Technologies Pvt. Ltd.