In the following diagram, what is the distance \(x\) if the radius of curvature is \(R= 15\text{cm}?\)

1.
\(30\text{cm}\)
2.
\(20\text{cm}\)
3.
\(15\text{cm}\)
4.
\(10\text{cm}\)

In the diagram shown below, the image of the point object \(O\) is formed at \(l\) by the convex lens of focal length \(20~\text{cm},\) where \(F_1\) and \(F_2\) are foci of the lens. The value of \(x'\) is:

| 1. | \(10~\text{cm}\) | 2. | \(20~\text{cm}\) |
| 3. | \(30~\text{cm}\) | 4. | \(40~\text{cm}\) |
A glass slab is placed with the right-angled prism as shown in the figure. The possible value of \(\theta\) such that light incident normally on the prism does not pass through the glass slab is:
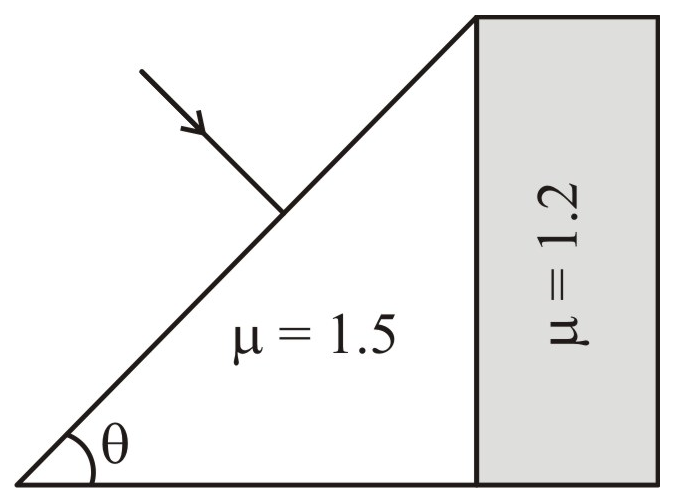
| 1. | \(30^\circ\) | 2. | \(37^\circ\) |
| 3. | \(45^\circ\) | 4. | Both (1) & (2) |
A graph is plotted between the angle of deviation \(\delta\) in a triangular prism and the angle of incidence as shown in the figure. Refracting angle of the prism is:
| 1. | \(28^\circ~\) | 2. | \(48^\circ~\) |
| 3. | \(36^\circ~\) | 4. | \(46^\circ~\) |
Three identical thin convex lenses are kept as shown in the figure. A ray passing through the lens is shown. The focal length of each lens is:

| 1. | \(5\) cm | 2. | \(10\) cm |
| 3. | \(15\) cm | 4. | \(20\) cm |
1. \(2\)
2. \(1.5\)
3. \(1.75\)
4. \(1.3\)
An astronomical telescope has angular magnification of \(20\) in its normal adjustment. Focal length of eyepiece is \(4\) cm. Distance between objective and eyepiece is:
| 1. | \(80\) cm | 2. | \(84\) cm |
| 3. | \(76\) cm | 4. | \(90\) cm |
If the space between two convex lenses of glass in the combination shown in the figure below is filled with water, then:

| 1. | the focal length of the system will decrease. |
| 2. | the focal length of the system will increase. |
| 3. | the power of the system will increase. |
| 4. | the power of the system will become infinite. |
The focal lengths of the objective and eyepiece of a compound microscope are \(2\text{cm}\) and \(6.25\text{cm}\) respectively. An object \(AB\) is placed at a distance of \(2.5\text{cm}\) from the objective which forms the image \(A'B'\) as shown in the figure. The maximum magnifying power in this case, will be:

| 1. | \(10\) | 2. | \(20\) |
| 3. | \(5\) | 4. | \(25\) |
A concave lens of focal length \(25~\text{cm}\) produces an image \(\frac{1}{10}\text{th}\) of the size of the object. The distance of the object from the lens is:
| 1. | \(225~\text{cm}\) | 2. | \(250~\text{cm}\) |
| 3. | \(150~\text{cm}\) | 4. | \(175~\text{cm}\) |






