A block of metal is heated to a temperature much higher than the room temperature and allowed to cool in a room free from air currents. Which of the following curves correctly represents the rate of cooling?
1.

2.

3.

4.





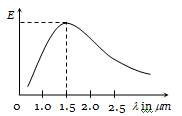
The energy distribution E with the wavelength for the black body radiation at temperature T Kelvin is shown in the figure. As the temperature is increased the maxima will:
| 1. | Shift towards left and become higher |
| 2. | Rise high but will not shift |
| 3. | Shift towards right and become higher |
| 4. | Shift towards left and the curve will become broader |
For a small temperature difference between the body and the surroundings, the relation between the rate of loss heat \(R\) and the temperature of the body \(\theta\) is depicted by:
| 1. |  |
2. |  |
| 3. |  |
4. |  |
Heat is flowing through a conductor of length l from x = 0 to x = l. If its thermal resistance per unit length is uniform, which of the following graphs is correct ?
Radius of a conductor increases uniformly from left end to right end as shown in the figure.
The material of the conductor is isotropic and its curved surface is thermally isolated from its surrounding. Its ends are maintained at temperatures \(T_1\) and \(T_2~(T_1>T_2).\) If in steady state, heat flow rate is equal to \(H,\) then which of the following graphs is correct?
| 1. |  |
2. |  |
| 3. |  |
4. |  |
| 1. |  |
2. |  |
| 3. |  |
4. | Both 1 and 3 |
A hollow copper sphere S and a hollow copper cube C, both of negligible thin walls of same area, are filled with water at 90°C and allowed to cool in the same environment. The graph that correctly represents their cooling is -
In the figure, the distribution of energy density of the radiation emitted by a black body at a given temperature is shown. The possible temperature of the black body is
(1) 1500 K
(2) 2000 K
(3) 2500 K
(4) 3000 K
Which of the following is the v/s T graph for a perfectly black body ( = frequency of peak radiation) ?
(1) A
(2) B
(3) C
(4) D
The spectrum of a black body at two temperatures 27 and 327 is shown in the figure. Let and be the areas under the two curves respectively. The value of is
(a) 1 : 16
(b) 4 : 1
(c) 2 : 1
(d) 16 : 1