An electric dipole is situated in an electric field of uniform intensity E whose dipole moment is p and moment of inertia is I. If the dipole is displaced slightly from the equilibrium position, then the angular frequency of its oscillations is?
1.
2.
3.
4.
An infinite number of electric charges each equal to \(5\) nC (magnitude) are placed along the \(x\text-\)axis at \(x=1\) cm, \(x=2\) cm, \(x=4\) cm, \(x=8\) cm ………. and so on. In the setup if the consecutive charges have opposite sign, then the electric field in Newton/Coulomb at \(x=0\) is: \(\left(\frac{1}{4 \pi \varepsilon_{0}} = 9 \times10^{9} ~\text{N-m}^{2}/\text{C}^{2}\right)\)
1. \(12\times 10^{4}\)
2. \(24\times 10^{4}\)
3. \(36\times 10^{4}\)
4. \(48\times 10^{4}\)
Three charges –q1, +q2 and –q3 are placed as shown in the figure. The x-component of the force on –q1 is proportional to
(1)
(2)
(3)
(4)
Two-point charges \(+q\) and \(–q\) are held fixed at \((–d, 0)\) and \((d, 0)\) respectively of a \((x, y)\) coordinate system. Then:
| 1. | \(E\) at all points on the \(y\text-\)axis is along \(\hat i\) |
| 2. | The electric field \(\vec E \) at all points on the \(x\text-\)axis has the same direction |
| 3. | The dipole moment is \(2qd\) directed along \(\hat i\) |
| 4. | The work has to be done to bring a test charge from infinity to the origin |
A point charge of \(40~\text{stat coulomb }\)is placed \(2~\text{cm}\) in front of an earthed metallic plane plate of large size. Then the force of attraction on the point charge is
1. \(100~\text{dynes}\)
2. \(160~\text{dynes}\)
3. \(1600~\text{dynes}\)
4. \(400~\text{dynes}\)
Which of the following graphs shows the variation of electric field E due to a hollow spherical conductor of radius R as a function of distance from the centre of the sphere
| 1. |  |
2. |  |
| 3. |  |
4. |  |
(1)
(2)
(3)
(4)
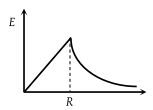
The electric field due to a uniformly charged solid sphere of radius R as a function of the distance from its centre is represented graphically by -
(1) 
(3) 
The electric field inside a spherical shell of uniform surface charge density is -
1. Zero
2. Constant, less than zero
3. Directly proportional to the distance from the centre
4. None of the above
The distance between charges 5 × 10–11 C and –2.7 × 10–11 C is 0.2 m. The distance at which a third charge should be placed in order that it will not experience any force along the line joining the two charges is
1. 0.44 m
2. 0.65 m
3. 0.556 m
4. 0.350 m
Suppose the charge of a proton and an electron differ slightly. One of them is \(\text- e\) and the other is \((e+\Delta e)\). If the net of electrostatic force and gravitational force between two hydrogen atoms placed at a distance \(d\) (much greater than atomic size) apart is zero, then \(\Delta e\)
1. \(10^{-20}~\text{C}\)
2. \(10^{-23}~\text{C}\)
3. \(10^{-37}~\text{C}\)
4. \(10^{-47}~\text{C}\)