A mass of \(4\) kg is suspended as shown in the figure with the help of massless inextensible string \(A\).
Another identical string, \(B\), is connected at the lower end of the block. When a sudden pulling downward jerk slightly greater than the breaking strength of \(A\) and \(B\) is given to string \(B\), then:

1.
String \(A\) will break.
2.
String \(B\) will break.
3.
Both \(A\) and \(B\) will break simultaneously.
4.
Both \(A\) and \(B\) will never break.

A \(0.5\) kg body experiences a force \(F=(2+3x^2)\) N, where \(x\) in metres is the displacement from the origin. If it is released to move along the \(X\)-axis from the origin, then its initial acceleration is:
| 1. | \(2~\text{m/s}^2\) | 2. | \(10~\text{m/s}^2\) |
| 3. | \(4~\text{m/s}^2\) | 4. | zero |
On the application of an impulsive force, a sphere of mass \(500\) grams starts moving with an acceleration of \(10\) m/s2. The force acts on it for \(0.5\) s. The gain in the momentum of the sphere will be:
1. \(2.5\) kg-m/s
2. \(5\) kg-m/s
3. \(0.05\) kg-m/s
4. \(25\) kg-m/s
What will be the reading of the spring balance in the given setup? (take \(g=10~\text{m/s}^2\) )

1. \(60~\text N\)
2. \(40~\text N\)
3. \(50~\text N\)
4. \(80~\text N\)
A bucket full of water tied with the help of a \(2\) m long string performs a vertical circular motion. The minimum angular velocity of the bucket at the uppermost point so that water will not fall will be:
1. \(2\sqrt{5}\) rad/s
2. \(\sqrt{5}\) rad/s
3. \(5\) rad/s
4. \(10\) rad/s
A motorcyclist is maintaining constant speed while going on an overbridge of radius R. When the motorcycle is ascending on the overbridge, the normal reaction on it
1. Increases
2. Remains the same
3. Decreases
4. Initially increases upto 45° with vertical and then decreases
A solid sphere of mass 2 kg is resting inside a cube as shown in the figure. The cube is moving with a velocity m/s. Here t is the time in second. All surface are smooth. The sphere is at rest with respect to the cube. What is the total force exerted by the sphere on the cube. (Take g = 10 m/s)
Two wooden blocks are moving on a smooth horizontal surface such that the mass m remains stationary with respect to block of mass M as shown in the fig. The magnitude of force P is

1. (M + m) g tan
2. g tan
3. (M + m) g cosec
4. mg cos
All surface shown in figure are smooth. System is released with the spring unstretched. In equilibrium, compression in the spring will be:
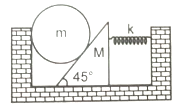
1.
2.
3.
4.
Figure shows two blocks, each of mass m. The system is released form rest. If accelerations of blocks A and B at any instant (not initially) are and , respectively, then
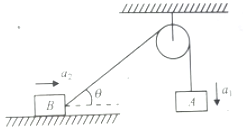
1.
2.
3.
4. None of these







