Please be patient as the PDF generation may take upto a minute.

Two discs A and B are rotating about parallel axes passing through their centres P and Q and perpendicular to the plane of discs. If their no slipping at the contact then
              
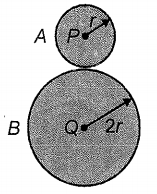
1  Angular speed of A and B are same
2  Angular speed of A is more than that of B
3  Angular speed of A is less than that of B  
4  Angular speed of A is half of angular speed of B

Three thin identical rods of mass 'M'and length 'L' each are connected to form a shape as shown in figure. The moment of inertia of this arrangement about an axis YY' is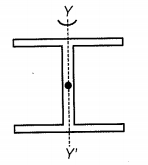

1  $\frac{M{L}^2}{4}$
2  $\frac{M{L}^2}{3}$
3  $\frac{M{L}^2}{2}$
$$
4  $\frac{M{L}^2}{6}$

Three masses \(m,\) \(2m,\) and \(3m\) are thrown from the top of a tower such that \(m\) is thrown vertically upward with \(10\) m/s, \(2m\) is thrown horizontally with \(15\) m/s and \(3m\) is thrown vertically downward with \(5\) m/s. The acceleration of centre of mass of the three-body system will be:
1. \(2\sqrt{2}g\)
2. \(g\)
3. \(\sqrt{2}g\)
4. zero

Moment of inertia of a uniform rod of length L and mass m about an axis through one end at an angle 45$°$ to rod is
1  $\frac{m{L}^2}{6}$
2  $\frac{m{L}^2}{3}$
3  $\frac{m{L}^2}{12}$
4  $\frac{m{L}^2}{4}$

Force is applied tangentially on the topmost point of ring kept on a rough horizontal surface such that rolls without slipping. Force of friction acting on it, is
                     
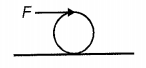
1  Horizontally backward
2  Horizontally forward
3  May be horizontally forward or backward
4  Zero

A ring of mass M and radius R is rolling with angular speed $\omega$ on a horizontal plane as shown in the figure. The angular momentum of the disc about point P is 
                    
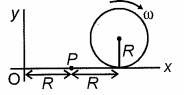
1  $M{R}^2\omega$
2  $\frac{M{R}^2\omega }{2}$
3  $2M{R}^2\omega$
4  $\sqrt{2}M{R}^2\omega$

A section of mass M and radius R is cut from a uniform circular disc. Its moment of inertia about an axis AA' passing through its centre perpendicular to its plane is
                 
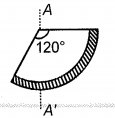
1  $\frac{M}{3}{R}^2$
2  $\frac{M}{6}{R}^2$
3  ${\frac{MR}{2}}^2$
4  MR²

The ball is rolling without slipping as shown in figure, then it reaches to the height of (no loss of energy in the bend)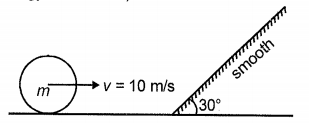

1  10 m
2  5 m
3  2 m
4  20 m

A man throws a rotating disc of mass m in upward direction. The velocity of centre of mass of disc is 20 m/s. If the disc is rotating about its axis perpendicular to the plane and axis is horizontal, then the time after which its velocity of centre of mass becomes equal and opposite to the initial is (neglect air friction, g = 10m/s²)
1  4 s
2  Less than 4 s
3  Greater than 4 s
4  Less or greater than 4 s depend on the direction of angular velocity of disc

Two body A and B are released from distance 5a. The masses of the bodies are 2m and 3m respectively. If these are moving due to mutual attraction then the distance covered by the body A before collision is
                
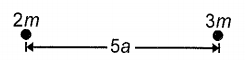
1  3a
2  2a
3  5a
4  a

A cubical block of mass m and side a rests on a rough inclined plane making an angle $\theta$ with the horizontal. The torque of reaction force about the centre of mass of the block is
1  $\frac{amg \sin \theta }{2}$
2  $amg \sin \theta$
3  $2amg \sin \theta$
4  $\frac{amg \cos \theta }{2}$

A ring of mass m and radius R is rolling without slipping with speed of the centre v, on a horizontal surface. The ring collides elastically with a smooth vertical wall. The angular momentum of the ring just after collision about the point of contact on the horizontal surface, is
1  mvR
2  2 mvR
3  3 mvR
4  Zero

A ladder of lenght I and negligible weight leans against a smooth wall at an angle $\theta$ with the horizontal. If $\mu$ is the coefficient of friction at the bottom, then the maximum distance from the contact point upto which a person can climb before the ladder slips, is
1  $\mu I \tan \theta$
2  $\mu I \cos \theta$
3  $\mu I \sin \theta$
4  $\mu I cot\theta$

A ball of mass m and radius r is tied to a string of length L. If it revolves in a horizontal circle with constant angular speed $\omega$, when the magnitude of torque acting on it is
1  Zero
2  $\frac{mvr}{L}$
3  $\left(\frac{m{v}^2}{L}r\right)$
4  $\frac{m{v}^2}{r}L$

A hollow sphere and a solid sphere are released on a rough inclined plane. Assume no slipping between the spheres and the plane. If v₁ and v₂ is the velocity of centre of mass at the bottom position respectively then
1  $v_1 > v_2$
2  $v_1 < v_2$
3   $v_1 = v_2$
4   $v_1 = 2v_2$