A particle is moving along the x-axis under a conservative force and its potential energy U varies with x co-ordinate as shown in the figure. Then force is positive at:
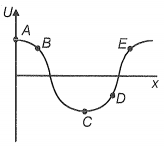
(1) A
(2) C, D
(3) B
(4) D, E
The potential energy \(\mathrm{U}\) of a system is given by (where \(\mathrm{x}\) is the position of its particle and \(\mathrm{A},\) \(\mathrm{B}\) are constants). The magnitude of the force acting on the particle is:
1. constant
2. proportional to \(\mathrm{x}\)
3. proportional to
4. proportional to
If U is the potential energy of a particle and x is its displacement, then in the position of stable equilibrium,
1.
2.
3.
4. All of these
The given plot shows the variation of U, the potential energy of interaction between two particles with the distance separating them, r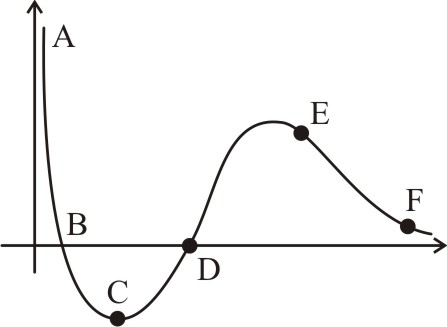
1. B and D are equilibrium points
2. C is a point of stable equlibrium
3. The force of interaction between the two particles is attractive between points C and D and repulsive between points D and E on the curve.
4. The force of interaction between the particles is attractive between points E and F on the curve.
A particle located in a one-dimensional potential field has its potential energy function as , where a and b are positive constants. The position of equilibrium x corresponds to
1.
2.
3.
4.
The figure shows how the potential energy \((U)\) of a particle varies with its position \(x.\) The particle moves under the influence of a conservative force along the \(x\)-axis.
| Statement I: | If the particle is released from rest at the origin \((x=0),\) it will start moving in the negative \(x\)-direction. |
| Statement II: | The positions \(x = 5~\text{m}\) and \(x =- 5~\text{m}\) are both stable equilibrium points of the particle. |
| 1. | Statement I is correct only. |
| 2. | Statement II is correct only. |
| 3. | Both statements are correct. |
| 4. | Both statements are incorrect. |
The points of maximum and minimum attraction in the curve between potential energy (U) and distance (r) of a diatomic molecules are respectively -
(1) S and R
(2) T and S
(3) R and S
(4) S and T
A particle free to move along the x-axis has potential energy given by for , where k is a positive constant of appropriate dimensions. Then
(1) At point away from the origin, the particle is in unstable equilibrium
(2) For any finite non-zero value of x, there is a force directed away from the origin
(3) If its total mechanical energy is k/2, it has its minimum kinetic energy at the origin
(4) For small displacements from x = 0, the motion is simple harmonic