A substance is in the solid form at \(0^{\circ}\text{C}\). The amount of heat added to this substance and its temperature are plotted in the following graph. If the relative specific heat capacity of the solid substance is \(0.5\), find from the graph, the specific heat of the substance in the liquid state is
(Specific heat capacity of water = \(1000~\text{cal kg}^{-1}\text{K}^{-1}\))
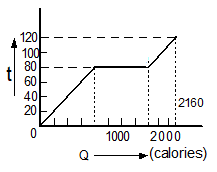
1. \(300~\text{cal kg}^{-1}\text{K}^{-1}\)
2. \(500~\text{cal kg}^{-1}\text{K}^{-1}\)
3. \(700~\text{cal kg}^{-1}\text{K}^{-1}\)
4. \(100~\text{cal kg}^{-1}\text{K}^{-1}\)
80 gm of water at 30°C is poured on a large block of ice at 0°C. The mass of ice that melts
(1) 30 gm
(2) 80 gm
(3) 1600 gm
(4) 150 gm
Minimum amount of steam of required to melt 12 gm ice completely will be
1. 1.5 gm
2. 1 gm
3. 2 gm
4. 5 gm
The temperature of a body on the Kelvin scale is found to be \(x^\circ~\text K.\) When it is measured by a Fahrenheit thermometer, it is found to be \(x^\circ~\text F,\) then the value of \(x\) is:
1. \(40\)
2. \(313\)
3. \(574.25\)
4. \(301.25\)
On a new scale of temperature (which is linear) and called the W scale, the freezing and boiling points of water are and respectively. What will be the temperature on the new scale, corresponding to a temperature of on the Celsius scale?
1.
2.
3.
4.
A thin copper wire of length L increases in length by 1% when heated from temperature . What is the percentage change in area when a thin copper plate having dimensions 2LL is heated from ?
1. 1%
2. 2%
3. 3%
4. 4%
A metal bar of length \(L\) and area of cross-section \(A\) is clamped between two rigid supports. For the material of the rod, it's Young’s modulus is \(Y\) and the coefficient of linear expansion is \(\alpha.\) If the temperature of the rod is increased by \(\Delta t^{\circ} \text{C},\) the force exerted by the rod on the supports will be:
1. \(YAL\Delta t\)
2. \(YA\alpha\Delta t\)
3. \(\frac{YL\alpha\Delta t}{A}\)
4. \(Y\alpha AL\Delta t\)
Two conductor rods of same length, same area of cross-section and having coefficient of thermal conductivities and respectively are arranged in series combination. Equivalent thermal conductivity of the combination is
1.
2.
3.
4.
Two ends of a conducting rod of varying cross-section are maintained at and as shown in Figure. In steady state,
1. Temperature difference across AB and CD are equal
2. Temperature difference across AB is greater than that across CD
3. Temperature difference across AB is less than that across CD.
4. Data is not sufficient to predict any of the above statements.
The power radiated by a black body is P, and it radiates maximum energy around the wavelength . If the temperature of black body is now changed so that it radiates maximum energy around a wavelength , the power radiated by it will increase by a factor of
1.
2.
3.
4.
A body cools from a temperature of \(3T\) to \(2T\) in \(10\) minutes. The room temperature is \(T.\) Assuming that Newton's law of cooling is applicable, the temperature of the body at the end of the next \(10\) minutes will be:
| 1. | \(\frac{7}{4}T\) | 2. | \(\frac{3}{2}T\) |
| 3. | \(\frac{4}{3}T\) | 4. | \(T\) |
A hollow copper sphere S and a hollow copper cube C, both of negligible thin walls of same area, are filled with water at 90°C and allowed to cool in the same environment. The graph that correctly represents their cooling is -
Heat is flowing through a conductor of length l from x = 0 to x = l. If its thermal resistance per unit length is uniform, which of the following graphs is correct ?
The energy distribution E with the wavelength for the black body radiation at temperature T Kelvin is shown in the figure. As the temperature is increased the maxima will:
| 1. | Shift towards left and become higher |
| 2. | Rise high but will not shift |
| 3. | Shift towards right and become higher |
| 4. | Shift towards left and the curve will become broader |
When a block of iron floats in Hg at , a fraction of its volumen= is submerged, while at temperature of a fraction is seen to be submersed. If the coefficient of volume expansion of iron is and that of mercury is , then the ratio can be expressed as:
1.
2.
3.
4.