Please be patient as the PDF generation may take up to a minute.

1.

On a new scale of temperature, which is linear and called the \(\text{W}\) scale, the freezing and boiling points of water are \(39^\circ ~\text{W}\) and \(239^\circ ~\text{W}\) respectively. What will be the temperature on the new scale corresponding to a temperature of \(39^\circ ~\text{C}\) on the Celsius scale?
1. \(78^\circ ~\text{W}\)
2. \(117^\circ ~\text{W}\)
3. \(200^\circ ~\text{W}\)
4. \(139^\circ ~\text{W}\)

2.

The coefficients of linear expansion of brass and steel rods are \(\alpha_1\) and \(\alpha_2\), lengths of brass and steel rods are \(l_1\) and \(l_2\) respectively. If (\(l_2-l_1\)) is maintained the same at all temperatures, Which one of the following relations holds good?
1. \(\alpha_1 l_2^2=\alpha_2l_1^2\)
2. \(\alpha_1^2 l_2=\alpha_2^2l_1\)
3. \(\alpha_1 l_1=\alpha_2l_2\)
4. \(\alpha_1 l_2=\alpha_2l_1\)

3.

The temperature of a wire of length \(1~\text{m}\) and an area of cross-section \(1~\text{cm}^2\) is increased from \(0^{\circ} \text {C}\) to \(100^{\circ} \text {C}.\) If the rod is not allowed to increase in length, the force required will be:
\((\alpha = 10^{-5}/ ^{\circ} \text {C} ~\text{and} ~Y = 10^{11} ~\text{N/m}^2)\)

1.	\(10^3 ~\text{N} \)	2.	\(10^4~\text{N} \)
3.	\(10^5 ~\text{N} \)	4.	\(10^9~\text{N} \)

4.

Liquid oxygen at \(50~\text K\) is heated up to \(300~\text K\) at a constant pressure of \(1~\text{atm}.\) The rate of heating is constant. Which one of the following graphs represents the variation of temperature with time?

1.		2.
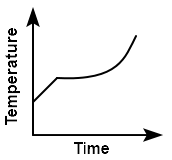3.		4.

5.

The two ends of a metal rod are maintained at temperatures \(100^{\circ}\mathrm{C}\) and \(110^{\circ}\mathrm{C}\). The rate of heat flow in the rod is found to be 4.0 J/s. If the ends are maintained at temperatures \(200^{\circ}\mathrm{C}\) and \(210^{\circ}\mathrm{C}\), the rate of heat flow will be:
1. 44.0 J/s
2. 16.8 J/s
3. 8.0 J/s
4. 4.0 J/s

6. Given below are two statements: 

Assertion (A):	While measuring the thermal conductivity of liquid experimentally, the upper layer is kept hot and the lower layer is kept cold.
Reason (R):	This avoids the heating of liquid by convection.

 

1.	Both (A) and (R) are True and (R) is the correct explanation of (A).
2.	Both (A) and (R) are True but (R) is not the correct explanation of (A).
3.	(A) is True but (R) is False.
4.	Both (A) and (R) are False.

7.

According to Wein's law:
1. ${\mathrm{\lambda }}_{\mathrm{m}}\mathrm{T}$= constant                 
2. $\frac{{\mathrm{\lambda }}_{\mathrm{m}}}{\mathrm{T}}$= constant
3. $\frac{T}{{\mathrm{\lambda }}_{\mathrm{m}}}$= constant                 
4. $\mathrm{T}+{\mathrm{\lambda }}_{\mathrm{m}}$= constant

8.

A black body has a maximum wavelength at a temperature of \(2000~\text K.\) Its corresponding wavelength at temperatures of \(3000~\text K\) will be: 

1.	\(\dfrac{3}{2} \lambda_m\)	2.	\(\dfrac{2}{3} \lambda_m\)
3.	\(\dfrac{4}{9} \lambda_m\)	4.	\(\dfrac{9}{4} \lambda_m\)

9. If the radius of a star is \(R\) and it acts as a black body, what would be the temperature of the star at which the rate of energy production is \(Q?\)\(\left(\sigma~ \text{is Stefan-Boltzmann constant}\right)\)

1.	\(\dfrac{Q}{4\pi R^2\sigma}\)	2.	\(\left(\dfrac{Q}{4\pi R^2\sigma}\right )^{\dfrac{-1}{2}}\)
3.	\(\left(\dfrac{4\pi R^2 Q}{\sigma}\right )^{\dfrac{1}{4}}\)	4.	\(\left(\dfrac{Q}{4\pi R^2 \sigma}\right)^{\dfrac{1}{4}}\)

10.

The temperature of a body falls from \(50^{\circ}\text{C}\)$\mathrm{}$ to \(40^{\circ}\text{C}\)$\mathrm{}$ in \(10\) minutes. If the temperature of the surroundings is \(20^{\circ}\text{C},\)$\mathrm{<mspace\; width="1em"></mspace>t}$hen the temperature of the body after another \(10\) minutes will be:
1. \(36.6^{\circ}\text{C}\)          
2. \(33.3^{\circ}\text{C}\)$\mathrm{}$
3. \(35^{\circ}\text{C}\)             
4. \(30^{\circ}\text{C}\)$\mathrm{}$