Motion in Straight line - Mind Map based Questions

1.

A ball is thrown upward with a certain speed. It passes through the same point at 3 second and 7 second from the start. The maximum height achieved by the ball is:
1. 500 m
2. 250 m
3. 125 m
4. 450 m

2.

For the following acceleration versus time graph the corresponding velocity versus displacement graph is:

1.		2.
3.		4.

3.

The acceleration $a$ (in ${ms}^{- 2}$ ) of a body, starting from rest varies with time $t$ (in $\mathrm{s}$) as per the equation $a=3t+4.$ The velocity of the body at time $t=2$ $\mathrm{s}$ will be:

1.	$10~\text{ms}^{-1}$	2.	$18~\text{ms}^{-1}$
3.	$14~\text{ms}^{-1}$	4.	$26~\text{ms}^{-1}$

4.

A stone falls freely from rest from a height h and it travels a distance $\frac{9 h}{25}$ in the last second. The value of h is:
1. 145 m
2. 100 m
3. 125 m
4. 200 ms

5.

A point moves in a straight line under the retardation $av^2$. If the initial velocity is $u,$ the distance covered in $t$ seconds is:
1. $(aut)$
2. $\frac{1}{a}\mathrm{ln}(aut)$
3. $\frac{1}{a}\mathrm{ln}(1+aut)$
4. $a~\mathrm{ln}(aut)$

6.

A body starts from the origin and moves along the X-axis such that the velocity at any instant is given by $(4 t^{3} - 2 t)$ , where t is in sec and velocity in m/s. What is the acceleration of the particle, when it is 2 m from the origin ?
1. 28 m/s²
2. 22 m/s²
3. 12 m/s²
4. 10 m/s²

7.

The relation between time and distance is given by $t=\alpha x^2+\beta x,$ where $\alpha$ and $\beta$ are constants. The retardation, as calculated based on this equation, will be (assume $v$ to be velocity):
1. $2\alpha v^3$
2. $2\beta v^3$
3. $2\alpha\beta v^3$
4. $2\beta^2 v^3$

8.

The initial velocity of a particle is u (at t = 0) and the acceleration f is given by at. Which of the following relation is valid
1. $v = u + a t^{2}$
2. $v = u + a \frac{t^{2}}{2}$
3. $v = u + a t$
4. v = u

9.

The velocity of a body depends on time according to the equation $v = 20 + 0 .1 t^{2}$ . The body is undergoing
1. Uniform acceleration
2. Uniform retardation
3. Non-uniform acceleration
4. Zero acceleration

10.

Two cars $A$ and $B$ are travelling in the same direction with velocities $v_1$ and $v_2 (v_1>v_2)$. When the car $A$ is at a distance $d$ behind car $B$, the driver of the car $A$ applied the brake producing uniform retardation $a$. There will be no collision when:
1. $d< \dfrac{(v_1-v_2)^2}{2a}$
2. $d< \dfrac{v^2_1-v^2_2}{2a}$
3. $d> \dfrac{(v_1-v_2)^2}{2a}$
4. $d> \dfrac{v^2_1-v^2_2}{2a}$

11.

The displacement of a particle is given by $y = a + bt + ct^{2} - dt^{4}$. The initial velocity and acceleration are, respectively:

1.	$b, -4d$	2.	$-b,2c$
3.	$b, ~2c$	4.	$2c, -2d$

12.

Two trains travelling on the same track are approaching each other with equal speeds of 40 m/s. The drivers of the trains begin to decelerate simultaneously when they are just 2.0 km apart. Assuming the decelerations to be uniform and equal, the value of the deceleration to barely avoid collision should be
1. 11.8 m/s²
2. 11.0 m/s²
3. 1.6 m/s²
4. 0.8 m/s²

13.

The acceleration $a$ in m/s² of a particle is given by $a = 3 t^{2} + 2 t + 2$ where t is the time. If the particle starts out with a velocity, $u=2$ m/s at t = 0, then the velocity at the end of $2$ seconds will be:
1. $12$ m/s
2. $18$ m/s
3. $27$ m/s
4. $36$ m/s

14.

A particle moves along a straight line such that its displacement at any time $t$ is given by $S = t^{3} - 6 t^{2} + 3 t + 4$ metres. The velocity when the acceleration is zero is:

1.	$4$ ms^-1	2.	$-12$ ms⁻¹
3.	$42$ ms⁻¹	4.	$-9$ ms⁻¹

15.

The relation $3t = \sqrt{3x} + 6$ describes the displacement of a particle in one direction where $x$ is in metres and $t$ in seconds. The displacement, when velocity is zero, is:

1.	$24$ metres	2.	$12$ metres
3.	$5$ metres	4.	zero

16.

Equation of displacement for any particle is $s = 3 t^{3} + 7 t^{2} + 14 t + 8 m$ . Its acceleration at time t = 1 sec is
1. 10 m/s²
2. 16 m/s²
3. 25 m/s²
4. 32 m/s²

17.

Consider the acceleration, velocity and displacement of a tennis ball as it falls to the ground and bounces back. Directions of which of these changes in the process ?
1. Velocity only
2. Displacement and velocity
3. Acceleration, velocity and displacement
4. Displacement and acceleration

18.

A student is standing at a distance of $50$ metres from the bus. As soon as the bus begins its motion with an acceleration of $1$ ms^–2, the student starts running towards the bus with a uniform velocity $u$. Assuming the motion to be along a straight road, the minimum value of $u$, so that the student is able to catch the bus is:
1. $5$ ms^–1
2. $8$ ms^–1
3. $10$ ms^–1
4. $12$ ms^–1

19.

A body A moves with a uniform acceleration a and zero initial velocity. Another body B, starts from the same point moves in the same direction with a constant velocity v. The two bodies meet after a time t. The value of t is
1. $\frac{2 v}{a}$
2. $\frac{v}{a}$
3. $\frac{v}{2 a}$
4. $\sqrt{\frac{v}{2 a}}$

20.

If the velocity of a particle is given by $v = (180-16x)^{1/2}~\text{m/s}$, then its acceleration will be:

1.	zero	2.	$8$ m/s²
3.	$-8$ m/s²	4.	$4$ m/s²

21.

The displacement of a particle is proportional to the cube of time elapsed. How does the acceleration of the particle depends on time obtained
1. $a \propto t^{2}$
2. $a \propto t^{4}$
3. $a \propto t^{3}$
4. $a \propto t$

22.

Starting from rest, acceleration of a particle is $a = 2 (t - 1) .$ The velocity of the particle at $t = 5 s$ is:
1. 15 m/sec
2. 25 m/sec
3. 5 m/sec
4. None of these

23.

A man is 45 m behind the bus when the bus starts accelerating from rest with acceleration of 2.5 m/s². With what minimum velocity should the man start running to catch the bus?
1. 12 m/s
2. 14 m/s
3. 15 m/s
4. 16 m/s

24.

A ball of mass m₁ and another ball of mass m₂ are dropped from equal height. If time taken by the balls are t₁ and t₂ respectively, then
1. $t_{1} = \frac{t_{2}}{2}$
2. $t_{1} = t_{2}$
3. $t_{1} = 4 t_{2}$
4. $t_{1} = \frac{t_{2}}{4}$

25.

Velocity of a body on reaching the point from which it was projected upwards, is
1. $v = 0$
2. $v = 2 u$
3. $v = 0 .5 u$
4. $v = - u$

26.

From the top of a tower, a particle is thrown vertically downwards with a velocity of 10 m/s. The ratio of the distances, covered by it in the 3^rd and 2^nd seconds of the motion is (Take $g = 10 m / s^{2}$ )
1. 5 : 7
2. 7 : 5
3. 3 : 6
4. 6 : 3

27.

When a ball is thrown up vertically with velocity v₀, it reaches a maximum height of 'h'. If one wishes to triple the maximum height then the ball should be thrown with velocity
1. $\sqrt{3} v_{o}$
2. 3v₀
3. 9v₀
4. (3/2)v₀

28.

A particle starts from rest. Its acceleration $(a)$ versus time $(t)$ is as shown in the figure. The maximum speed of the particle will be:

1. $110~\text{m/s}$
2. $55~\text{m/s}$
3. $550~\text{m/s}$
4. $660~\text{m/s}$

29.

The variation of velocity of a particle with time moving along a straight line is illustrated in the following figure. The distance travelled by the particle in four seconds is

1. $60~\text m$
2. $55~\text m$
3. $25~\text m$
4. $30~\text m$

30.

The displacement of a particle as a function of time is shown in the figure. The figure shows that

1. The particle starts with certain velocity but the motion is retarded and finally the particle stops
2. The velocity of the particle is constant throughout
3. The acceleration of the particle is constant throughout
4. The particle starts with constant velocity, then motion is accelerated and finally the particle moves with another constant velocity

31.

A ball is thrown vertically upwards. Which of the following graph/graphs represent velocity-time graph of the ball during its flight (air resistance is neglected)

1. a
2. b
3. c
4. d

32.

The v – t graph of a moving object is given in the figure. The maximum acceleration is:

1. $1 c m / s e c^{2}$
2. $2 c m / s e c^{2}$
3. $3 c m / s e c^{2}$
4. $6 c m / s e c^{2}$

33.

Velocity-time curve for a body projected vertically upwards is
1. Parabola
2. Ellipse
3. Hyperbola
4. Straight line

34.

An object is moving with a uniform acceleration which is parallel to its instantaneous direction of motion. The displacement (s) – velocity (v) graph of this object is

1.
2.
3.
4.

35.

A ball is thrown vertically upwards. Which of the following plots represents the speed-time graph of the ball during its height if the air resistance is not ignored?

1.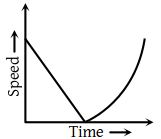
2.
3.
4.

36.

Which of the following velocity-time graphs shows a realistic situation for a body in motion?

1.		2.
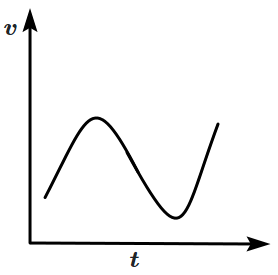3.		4.

37.

If the velocity of a particle is $v = At + {Bt}^{2}$ , where A and B are constants, then the distance travelled by it between 1s and 2s is?
$1 .$ $3 A + 7 B$
$2 .$ $\frac{3 A}{2} + \frac{7 B}{3}$
$3 .$ $\frac{A}{2} + \frac{B}{3}$
$4 .$ $\frac{A}{3} + \frac{B}{2}$

38.

A particle of unit mass undergoes one-dimensional motion such that its velocity varies according to v(x)= $β x^{- 2 n}$ where, $β$ and n are constants and x is the position of the particle. The acceleration of the particle as a function of x, is given by
1. $- 2 n β^{2} x^{- 2 n - 1}$
2. $- 2 n β^{2} x^{- 4 n - 1}$
3. $- 2 β^{2} x^{- 2 n + 1}$
4. $2 n β^{2} e^{- 4 n}$ ⁺¹

39.

A stone falls under gravity. It covers distances h₁, h₂and h₃ in the first 5 seconds, the next 5 seconds and the next 5 seconds respectively. The relation between h₁, h_2, and h₃ is
1. h₁=2h₂=3h₃
2. h₁=h₂/3=h₃/5
3. h₂=3h₁ and h3=3h₂
4. h₁=h₂=h₃

40.

The motion of a particle along a straight line is described by the equation; $x=8+12 t-t^3,$ where $x$ is in metre and $t$ is in second. The retardation of the particle when its velocity becomes zero is:

1.	$24 ~\text{ms}^{-2} $	2.	zero
3.	$ 6 ~\text{ms}^{-2} $	4.	$12 ~\text{ms}^{-2} $

41.

A boy standing at the top of a tower of $20$ m height drops a stone. Assuming $g=10$ m/s², the velocity with which it hits the ground will be:
1. $20$ m/s
2. $40$ m/s
3. $5$ m/s
4. $10$ m/s

42.

A ball is dropped from a high rise platform at t=0 starting from rest. After 6s another ball is thrown downwards from the same platform with a speed v. The two balls meet at t=18 s. What is the value of v? (take g=10 $m s^{- 2}$ )
1. $75 m s^{- 1}$ 2. $55 m s^{- 1}$
3. $40 m s^{- 1}$ 4. $60 m s^{- 1}$

43.

A particle moves a distance x in time t according to equation $x = {(t + 5)}^{- 1} .$ The acceleration of the particle is proportional to,
1. ${(v e l o c i t y)}^{3 / 2}$
2. ${(d i s \tan c e)}^{2}$
3. ${(d i s \tan c e)}^{- 2}$
4. ${(v e l o c i t y)}^{2 / 3}$

44.

A bus is moving with a speed of $10~\text{ms}^{-1}$ on a straight road. A scooterist wishes to overtake the bus in $100~\text{s}$. If the bus is at a distance of $1~\text{km}$ from the scooterist, with what minimum speed should the scooterist chase the bus?
1. $20~\text{ms}^{-1}$
2. $40~\text{ms}^{-1}$
3. $25~\text{ms}^{-1}$
4. $10~\text{ms}^{-1}$

45.

A particle shows a distance-time curve as given in this figure. The maximum instantaneous velocity of the particle is around the point:

1. B
2. C
3. D
4. A

Fill OMR Sheet*

*If above link doesn't work, please go to test link from where you got the pdf and fill OMR from there

CLICK HERE to get FREE ACCESS for 2 days of ANY NEETprep course

1.	\(10~\text{ms}^{-1}\)	2.	\(18~\text{ms}^{-1}\)
3.	\(14~\text{ms}^{-1}\)	4.	\(26~\text{ms}^{-1}\)

1.	\(4\) ms^-1	2.	\(-12\) ms⁻¹
3.	\(42\) ms⁻¹	4.	\(-9\) ms⁻¹

1.	\(24 ~\text{ms}^{-2} \)	2.	zero
3.	\( 6 ~\text{ms}^{-2} \)	4.	\(12 ~\text{ms}^{-2} \)

1.	\(b, -4d\)	2.	\(-b,2c\)
3.	\(b, ~2c\)	4.	\(2c, -2d\)

Please be patient as the PDF generation may take up to a minute.

Fill OMR Sheet*