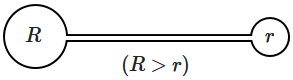Custom Practice Test

Physics

1. The temperature of a gas is \(-50^\circ \text{C}.\) To what temperature the gas should be heated so that the RMS speed is increased by \(3\) times?

1.	\(223~\text{K}\)	2.	\(669^\circ \text{C}\)
3.	\(3295^\circ \text{C}\)	4.	\(3097~\text{K}\)

2. Liquid drops are falling slowly one by one from a vertical glass tube. Establish a relation between the weight \(W\) of a drop, the surface tension \(T,\) and the radius \(r\) of the tube: \(\left({\mathit{\theta}{=}\mathop {0}\nolimits^{\circ}}\right)\)
1. \(W=\pi r^{2}T\)
2. \(W=2\pi rT\)
3. \(W=2\pi r^{2}T \)
4. \(W=\frac{4}{3}(\pi r^{3}T)\)

3.

A spring of force constant \(k\) is cut into lengths of ratio \(1:2:3\). They are connected in series and the new force constant is \(k'\). Then they are connected in parallel and the force constant is \(k''\). Then \(k':k''\) is:
1. \(1:9\)
2. \(1:11\)
3. \(1:14\)
4. \(1:6\)

4.

If the time period of a \(2\) m long simple pendulum is \(2\) s, the acceleration due to gravity at the place where the pendulum is executing simple harmonic motion is:
1. \(\pi^{2}\) m/s²
2. \(2\pi^{2}\) m/s²
3. \(9.8\) m/s²
4. \(16\) m/s²

5. Tanks \(A\) and \(B\) open at the top contains two different liquids upto a certain height in them. A hole is made in the wall of each tank at a depth \(h\) from the surface of the liquid. The area of the hole in \(A\) is twice that of in \(B\). If the mass flow rate through each hole is equal, then the ratio of densities of the liquids respectively is:

1.	\(\dfrac{2}{1}\)	2.	\(\dfrac{3}{2}\)
3.	\(\dfrac{2}{3}\)	4.	\(\dfrac{1}{2}\)

6. In which of the following processes does the internal energy of a gas remain constant?
1. Isothermal
2. Isochoric
3. Isobaric
4. Adiabatic

7.

Assuming the sun to have a spherical outer surface of radius \(r,\) radiating like a black body at temperature \(t^\circ \text{C},\) the power received by a unit surface of the earth (normal to the incident rays) at a distance \(R\) from the centre of the sun will be:
(where \(\sigma\) is Stefan's constant)

1.	\(\dfrac{4\pi r^2\sigma t^4}{R^2}\)	2.	\(\dfrac{r^2\sigma(t+273)^4}{4\pi R^2}\)
3.	\(\dfrac{16\pi^2r^2\sigma t^4}{R^2}\)	4.	\(\dfrac{r^2\sigma(t+273)^4}{R^2}\)

8.

A metal ball of mass \(2~\text{kg}\) is heated by a \(30~\text{W}\) heater, in a room at \(20^{\circ}\text{C}.\) The temperature of the metal becomes steady at \(50^{\circ}\text{C}.\) If the ball was kept in a room at \(20^{\circ}\text{C}\) while maintaining a temperature of \(10^{\circ}\text{C},\) the rate at which heat must be removed from the ball is:
1. \(20~\text{W}\)
2. \(10~\text{W}\)
3. \(5~\text{W}\)
4. \(1~\text{W}\)

9. The elongation of a wire on the surface of the Earth is \(10^{-4}\) m. The same wire, of the same dimensions, elongates by \( 6 \times 10^{-5} \) m on another planet. The acceleration due to gravity on the planet will be:
(take acceleration due to gravity on the surface of the Earth as \(10\) m s^-2)
1. \(5\) ms^-2
2. \(6\) ms^-2
3. \(7\) ms^-2
4. \(8\) ms^-2

10. A small thin tube is connected to two soap bubbles, one of radius \(R\) and the other radius \(r\) — so that the air in the two bubbles can flow through the tube. Then, air will flow:

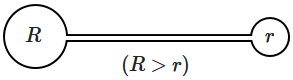
1.	from the larger bubble to the smaller bubble, until the two are of equal size.
2.	from the large bubble to the smaller bubble initially, and the smaller one becomes larger; then the flow is reversed.
3.	from the smaller bubble to the larger one until the smaller bubble becomes very small.
4.	from the larger to the smaller bubble and it bursts the smaller bubble.

11. Given below are two statements:

Assertion (A):	When height of a tube is less than liquid rise in the capillary tube, the liquid does not overflow.
Reason (R):	Product of radius of meniscus and height of liquid in capillary tube always remains constant.

1.	Both (A) and (R) are True and (R) is the correct explanation of (A).
2.	Both (A) and (R) are True but (R) is not the correct explanation of (A).
3.	(A) is True but (R) is False.
4.	(A) is False but (R) is True.

12. A gas in a vessel is initially at pressure \(P.\) If the mass of all the gas molecules is halved and their speed is doubled, then the resultant pressure will be:

1.	\(2 P\)	2.	\(P\)
3.	\(\dfrac{P}{2}\)	4.	\(4 P\)

13.

Given below are two statements:

Statement I:	It is impossible to convert all the heat energy into work.
Statement II:	A body's temperature can be increased without adding heat to it.

1.	Statement I is False but Statement II is True.
2.	Both Statement I and Statement II are True.
3.	Both Statement I and Statement II are False.
4.	Statement I is True but Statement II is False.

14.

A gas is compressed isothermally to half its initial volume. The same gas is compressed separately through an adiabatic process until its volume is again reduced to half. Then,

1.	compressing the gas through an adiabatic process will require more work to be done.
2.	compressing the gas isothermally or adiabatically will require the same amount of work.
3.	which of the case (whether compression through isothermal or through the adiabatic process) requires more work will depend upon the atomicity of the gas.
4.	compressing the gas isothermally will require more work to be done.

15. Two uniform rods, \(AB\) and \(BC,\) have Young's moduli of \(1.2~\times~ 10^{11}~ \text{N/m}^2\) and \(1.5~\times~ 10^{11}~ \text{N/m}^2,\) respectively. The coefficient of linear expansion for rod \(AB\) is \(1.5~\times~ 10^{-5} /^\circ \text{C}.\) If both rods have equal cross-sectional area, then the coefficient of linear expansion of \(BC,\) for which there is no shift of the junction at all temperatures, is:

1. \(1.5~\times~ 10^{-5} /^\circ \text{C}\)
2. \(1.2~\times~ 10^{-5} /^\circ \text{C}\)
3. \(0.6~\times~ 10^{-5} /^\circ \text{C}\)
4. \(0.75~\times~ 10^{-5} /^\circ \text{C}\)

16. A thermodynamic system is taken through the cycle \(abcda.\) The work done by the gas along the path \(bc\) is:

1. \(30~\text J\)
2. \(-90~\text J\)
3. \(-60~\text J\)
4. zero

17. A simple pendulum undergoing small oscillations of amplitude \(1~\text{cm},\) has a time period of \(2~\text{s}.\) If the amplitude of oscillation is halved, the time period will:

1.	remain unchanged
2.	increase to \(4~\text{s}\)
3.	decrease to \(1~\text{s}\)
4.	decrease to \(0.5~\text{s}\)

18. Consider the bob of a pendulum of mass \(M,\) suspended by a wire of length \(L,\) cross-section \(A.\) As the bob oscillates, it has a speed \(v,\) at its lowest point. The stress in the wire, at the lowest point, is:

1.	\(\Large\frac{Mg}{A}\)	2.	\(\dfrac{M}{A}\left({\small g}+\dfrac{v^2}{L}\right)\)
3.	\(\dfrac{M}{A}\left({\small g}-\dfrac{v^2}{L}\right)\)	4.	\(\dfrac{M}{A}\left({\small g}+\dfrac{v^2}{2L}\right)\)

19. A monoatomic gas \((A)\) and a diatomic gas \((B)\) are taken in two separate identical containers at the same conditions of temperature and pressure.
The two gases are allowed to expand slowly, isothermally, until their volumes are doubled. The final pressure of gas \(A\) is \(P_A\) and that of gas \(B\) is \(P_B.\) Then:

1.	\(P_A=P_B\)
2.	\(P_A=2P_B\)
3.	\(P_A=\dfrac{1}{2}P_B\)
4.	the relationship between \(P_A\) and \(P_B\) depends on the molecular weights of \(A\) and \(B\)

20.

A uniform metallic wire is elongated by \(0.04\) m when subjected to a linear force \(F\). The elongation, if its length and diameter are doubled and subjected to the same force will be:

1.	\(1\) cm	2.	\(2 \) cm
3.	\(3\) cm	4.	\(6\) cm

21. Given an ideal gas undergoing a process where the work done, \(dW=0\) and the heat transfer, \(dQ<0,\) what can be inferred about the gas?

1.	The temperature will decrease.
2.	The volume will increase.
3.	The pressure will remain constant.
4.	The temperature will increase.

22. During an experiment, an ideal gas is observed to obey the law: \(PV^3= \text{constant}\), as the process is conducted. If the volume of the gas doubles during this process, the absolute temperature of the gas changes from \(T\) to:
1. \(2T\)
2. \(4T\)
3. \(\dfrac T 2\)
4. \(\dfrac T 4\)

23. A rod of length \(L\) is pulled along its length by means of a pulling force \(F,\) which causes it to accelerate. The cross-section of the rod is uniform and equals \(A.\) The average stress in the rod equals:

1.	\(\dfrac{F}{A}\)	2.	\(\dfrac{F}{2A}\)
3.	\(\dfrac{F}{3A}\)	4.	\(\dfrac{F}{4A}\)

24.

A rectangular film of liquid is extended from \((4~\text{cm} \times 2~\text{cm})\) to \((5~\text{cm} \times 4~\text{cm}).\) If the work done is \(3\times 10^{-4}~\text J,\) then the value of the surface tension of the liquid is:
1. \(0.250~\text{Nm}^{-1}\)
2. \(0.125~\text{Nm}^{-1}\)
3. \(0.2~\text{Nm}^{-1}\)
4. \(8.0~\text{Nm}^{-1}\)

25.

The efficiency of an ideal heat engine (Carnot heat engine) working between the freezing point and boiling point of water is:
1. \(26.8\%\)
2. \(20\%\)
3. \(6.25\%\)
4. \(12.5\%\)

26.

If the radius of a star is \(R\) and it acts as a black body, what would be the temperature of the star at which the rate of energy production is \(Q?\)
\(\left(\sigma~ \text{is Stefan-Boltzmann constant}\right)\)
1. \(\dfrac{Q}{4\pi R^2\sigma}\)
2. \(\left(\dfrac{Q}{4\pi R^2\sigma}\right )^{\dfrac{-1}{2}}\)
3. \(\left(\dfrac{4\pi R^2 Q}{\sigma}\right )^{\dfrac{1}{4}}\)
4. \(\left(\dfrac{Q}{4\pi R^2 \sigma}\right)^{\dfrac{1}{4}}\)

27.

A spherical solid ball of volume \(V\) is made of a material of density \(\rho_1.\) It is falling through a liquid of density \(\rho_2(\rho_2<\rho_1)\) Assuming that the liquid applies a viscous force on the ball that is proportional to the square of its speed \(v,\) i.e., \(F_{\text{viscous}}=-kv^2(k>0),\) the terminal speed of the ball is:
1. \( \dfrac{{Vg} \rho_1}{k} \)
2. \( \sqrt{\dfrac{{Vg} \rho_1}{k}} \)
3. \( \dfrac{{Vg}\left(\rho_1-\rho_2\right)}{k} \)
4. \( \sqrt{\dfrac{{Vg}\left(\rho_1-\rho_2\right)}{k}} \)

28.

The time period of a simple pendulum in a stationary trolley is \(T_1.\) If the trolley is moving with a constant speed, then the time period is \(T_2.\) Then:
1. \(T_1>T _2\)
2. \(T_1<T _2\)
3. \(T_1=T _2\)
4. \(T_2= \infty \)

29. A particle performing simple harmonic motion with amplitude, \(A\) starts from \(x = 0\) and reaches \(x = A/2\) in \(2\) s. The time required for the particle to go from \(x = A/2\) to \(x = A\) is:

1.	\(1.5\) s	2.	\(4\) s
3.	\(6\) s	4.	\(1\) s

30. Given below are two statements:

Assertion (A):	When the pressure of a gas is increased by compressing it without any change in its temperature, the RMS speed of its molecules does not increase.
Reason (R):	The RMS speed of the molecules of an ideal gas is determined by its absolute temperature only: \(v_{\text{RMS}}=\sqrt{{\dfrac{3kT}{m}}} \).

1.	Both (A) and (R) are True and (R) is the correct explanation of (A).
2.	Both (A) and (R) are True but (R) is not the correct explanation of (A).
3.	(A) is True but (R) is False.
4.	(A) is False but (R) is True.

31.

Kinetic energy of an ideal gas is proportional to:
1. \(T\)
2. \(1 \over T\)
3. \(T^0\)
4. \(T^2\)

32.

The figure shows a pendulum at the bottom of its swing.

What is the direction of the acceleration vector for the bob?

1.		2.
3.		4.	There is no acceleration at this point.

33.

The pressure of an ideal gas is written as \(P=\dfrac{2E}{3V}\). Here \(E \) refers to:

1.	translational kinetic energy
2.	rotational kinetic energy
3.	vibrational kinetic energy
4.	total kinetic energy

34. Three identical \(4~\text{kg}\) blocks are placed one atop of the other, as shown in the figure, on a smooth horizontal plane. The system is placed in an elevator moving upward with an acceleration equal to \(g.\) Consider the three horizontal surfaces of contact ①, ②, ③, all of these having the same cross-sectional area. Let, the stresses at these surfaces be \(S_1,S_2,S_3.\) Then:

Statement I:	\(S_1,S_2,S_3\) increase when the elevator is accelerated upward.
Statement II:	The proportion \(S_1:S_2:S_3\) remains unchanged with acceleration.

1.	Statement I is incorrect and Statement II is correct.
2.	Both Statement I and Statement II are correct.
3.	Both Statement I and Statement II are incorrect.
4.	Statement I is correct and Statement II is incorrect.

35.

An object kept in a large room having an air temperature of \(25^\circ \text{C}\) takes \(12 ~\text{min}\) to cool from \(80^\circ \text{C}\) to \(70^\circ \text{C}.\) The time taken to cool for the same object from \(70^\circ \text{C}\) to \(60^\circ \text{C}\) would be nearly:
1. \(10 ~\text{min}\)
2. \(12 ~\text{min}\)
3. \(20 ~\text{min}\)
4. \(15 ~\text{min}\)

36. Air flows across the horizontal wings of an airplane in such a way that its speeds below and above the wings are \(90\) m/s and \(120\) m/s respectively. If the density of air is \(1.3\) kg/m³, then the pressure difference across the lower and upper radii of the wings will be:

1.	\(7338\) N/m²	2.	\(3715\) N/m²
3.	\(3220\) N/m²	4.	\(4095\) N/m²

37. A jar contains a mixture of hydrogen and oxygen gases in a \(1:5\) ratio. The ratio of the mean kinetic energy of hydrogen molecules to that of oxygen molecules is:

1.	\(1:16\)	2.	\(1:4\)
3.	\(1:5\)	4.	\(1:1\)

38. Three moles of oxygen and four moles of helium are mixed at room temperature. What is the degree of freedom of the mixture?
1. \(15\over 7\)
2. \(12\over 7\)
3. \(27\over 7\)
4. \(3\over 2\)

39. Given \(x=x_m\text{cos}(\omega t+\phi),\) if at \(t=0,\) \(x = x_m,\) then the time taken to reach \(x = \dfrac{x_m}{2}\) is:
(where \(T\) is the time period of the motion)
1. \(3T/2\)
2. \(T/3\)
3. \(2T/3\)
4. \(T/6\)

40. An ideal gas (\(\gamma=1.51\)) is expanded adiabatically. How many times has the gas to be expanded to reduce the root mean square velocity of molecules \(2.0\) times?
1. \(4\) times
2. \(16\) times
3. \(8\) times
4. \(2\) times

41.

During simple harmonic motion of a body, the energy at the extreme position is:

1.	both kinetic and potential
2.	is always zero
3.	purely kinetic
4.	purely potential

42. A piece of iron of water equivalent \(10 \) g is taken from a furnace and put into a calorimeter containing \(100\) g of water at an initial temperature of \(20^{\circ} \text{C}.\) The final temperature of the system is observed to be \(80^{\circ} \text{C}.\) Ignore the thermal capacity of the calorimeter and any loss of heat. The temperature of the furnace is:
1. \(600^{\circ} \text{C}\)
2. \(620^{\circ} \text{C}\)
3. \(680^{\circ} \text{C}\)
4. \(520^{\circ} \text{C}\)

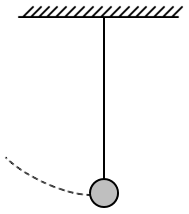
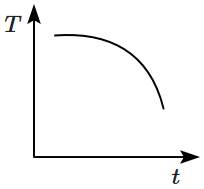
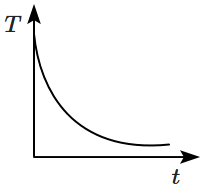
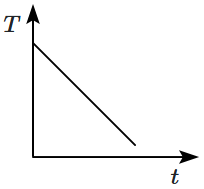
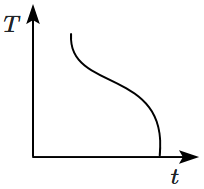
43. A metal block is heated to a temperature much higher than room temperature and is allowed to cool in a room free from air currents. Which of the following curves correctly represents the cooling process?
(\(T\) represents the temperature of the block and \(t\) represents time)

1.		2.
3.		4.

44. If the ratio of diameters, lengths and Young's modulus of steel and copper wires shown in the figure are \(p,\) \(q\) and \(s\) respectively, then the corresponding ratio of increase in their lengths would be:

1.	\(\dfrac{5 q}{\left(7 {sp}^2\right)} \)	2.	\(\dfrac{7 q}{\left(5 sp^2\right)} \)
3.	\(\dfrac{2 q}{(5 s p)} \)	4.	\(\dfrac{7 q}{(5 s p)}\)

45. The figure displays a graph depicting the relationship between stress and strain for a uniform wire at two distinct temperatures \(T_1~\text{&}~T_2.\)

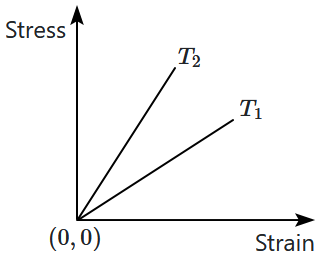
Based on the graph, which of the following conclusions can be drawn?
1. \(T_1 > T_2\)
2. \(T_2 > T_1\)
3. \(T_1 = T_2\)
4. None of the above.

Fill OMR Sheet*

*If above link doesn't work, please go to test link from where you got the pdf and fill OMR from there

CLICK HERE to get FREE ACCESS for 2 days of ANY NEETprep course

Please be patient as the PDF generation may take up to a minute.

Fill OMR Sheet*