Please be patient as the PDF generation may take upto a minute.

1.

A bob of mass m attached to an inextensible string of length l is suspended from vertical support.  The bob rotates in a horizontal circle with an angular speed $\mathrm{\omega }$ $\mathrm{rad}/\mathrm{s}$ about the vertical.  About the point of suspension.

1.	Angular momentum is conserved
2.	Angular momentum changes in magnitude but not in the direction
3.	Angular momentum changes in direction but not in magnitude
4.	Angular momentum changes both in direction and magnitude

2.

The figure shows a small wheel fixed coaxially on a bigger one of double the radius. The system rotates about the common axis. The strings supporting A and B do not slip on the wheels. If x and y be the distances traveled by A and B in the same time interval, then
                          
1. x-2y
2. x = y
3. y=2x
4. none of these

3.

If rotational kinetic energy is 50 % of translational kinetic energy, then the body is 
1. Ring
2. Cylinder
3. Hollow sphere
4. Solid sphere

4.

If the radius of the earth is suddenly contracted to half of its present value, then the duration of the day will be of:

1.	6 hours	2.	12 hours
3.	18 hours	4.	24 hours

5.

A sphere can not roll on:
1.  a smooth horizontal surface 
2.  a rough horizontal surface 
3.  a smooth inclined surface 
4.  a rough inclined surface 

6.

A cord is wound round the circumference of wheel of radius r. The axis of the wheel is horizotal and moment of inertia about it is I. A weight mg is attached to the end of the cord and falls from rest. After falling through a distance h, the angular velocity of the wheel will be
1. $\sqrt{\frac{2gh}{I+mr}}$
2. $\sqrt{\frac{2mgh}{I+m{r}^2}}$
3. ${\left[\frac{2mgh}{I+2m}\right]}^{\frac{1}{2}}$
4. $\sqrt{2gh}$

7.

A solid cylinder and a solid sphere, both having the same mass and radius, are released from a rough inclined plane. Both roll without slipping. Then,
1.  the force of friction that acts on the two is the same
2.  the force of friction is greater in the case of a sphere than in a cylinder
3.  the force of friction is greater in the case of a cylinder than in a sphere
4.  the force of friction will depend on the nature of the surface of the body that is moving and that of the inclined surface and is independent of the shape and size of the moving body

8.

A rigid body rotates about a fixed axis with a variable angular velocity equal to \(\alpha -\beta t\), at the time \(t\), where \(\alpha , \beta\) are constants. The angle through which it rotates before it stops is:

1.	\(\frac{\alpha^{2}}{2 \beta}\)	2.	\(\frac{\alpha^{2} -\beta^{2}}{2 \alpha}\)
3.	\(\frac{\alpha^{2} - \beta^{2}}{2 \beta}\)	4.	\(\frac{\left(\alpha-\beta\right) \alpha}{2}\)

9.

One hollow and one solid cylinder of the same radius roll down on a smooth inclined plane. Then the foot of the inclined plane is reached by 
1.  solid cylinder earlier 
2.  hollow cylinder earlier 
3.  simultaneously both 
4.  the heavier earlier irrespective of being solid or hollow

10. A circular platform is mounted a frictionless vertical axle. Its radius \(R= 2~\text{m}\) and moment of inertia about the axle are \(200~\text{kgm}^2\)${\mathrm{}}^{}$. It is initially at rest. A \(50~\text{kg}\) man on the edge of the platform and begins to walk along the edge at the speed of \(1~\text{ms}^{-1}\) relative to the ground. Time taken by the man to complete one revolution is:
1. \(\pi~\text{s}\)
2. \(\frac{3\pi}{2}~\text{s}\)
3. \(2\pi~\text{s}\)
4. \(\frac{\pi}{2}~\text{s}\)

11.

A uniform rod AB of length l and mass m is free to rotate about point A. The rod is released from rest in horizontal position. Given that the moment of inerita of the rod about A is $\frac{{\mathrm{ml}}^2}{3}$ the initial angular acceleration of the rod will be
                           
$1. \frac{2\mathrm{g}}{3\mathrm{l}}$
$2. \mathrm{mg}\frac{\mathrm{l}}{2}$
$3. \frac{3}{2}\mathrm{gl}$
$4. \frac{3\mathrm{g}}{2\mathrm{l}}$

12.

The disc is placed on the rough horizontal surface given only angular velocity ${\omega }_0$. The velocity of the centre of mass when it starts pure rolling is:
1.  $\frac{{\omega }_{0}R}{2}$
2.  $\frac{{\omega }_{0}R}{3}$
3.  $\frac{{\omega }_{0}R}{4}$
4.  $\frac{{\omega }_{0}R}{6}$

13.

A force 2N is along line y = 3x + 4. The torque about the origin is:
1.  $\frac{5}{\sqrt{10}}\mathrm{Nm}$
2.  $\frac{7}{\sqrt{10}}\mathrm{Nm}$
3.  $\frac{6}{\sqrt{10}}\mathrm{Nm}$
4.  $\frac{8}{\sqrt{10}}\mathrm{Nm}$

14.

The moment of inertia of pulley is I and its radius is R. The string doesn't slips on the pulley, as system is released, the acceleration of the system is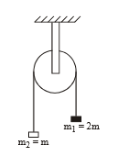

1. $\frac{g}{\left(3+{\displaystyle \frac{I}{m{R}^2}}\right)}$
2. $\frac{g}{\left(1+{\displaystyle \frac{I}{m{R}^2}}\right)}$
3. $\frac{3g}{\left(1+{\displaystyle \frac{I}{m{R}^2}}\right)}$
4. $\frac{3g}{\left(2+{\displaystyle \frac{I}{m{R}^2}}\right)}$

15.

Two discs of same moment of inertia rotating about their regular axis passing through centre and perpendicular to the plane of disc with angular velocities ${\omega }_{1 } and {\omega }_2$. They are brought into contact face to face coinciding the axis of rotation.  The expression for loss of energy during this process is 
1. $\frac{1}{2}I{\left({\omega }_1+{\omega }_2\right)}^2$
2. $\frac{1}{4}I{\left({\omega }_1-{\omega }_2\right)}^2$
3. $I{\left({\omega }_1-{\omega }_2\right)}^2$
4. $\frac{1}{8}I{\left({\omega }_1-{\omega }_2\right)}^2$