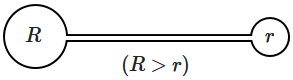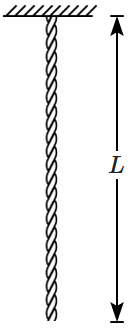Physics - Section A
1. A square aluminium (shear modulus is
\(25\times10^{9}~\text{Nm}^{-2}\)) slab of side
\(60~\text{cm}\) and thickness of
\(15~\text{cm}\) is subjected to a shearing force (on its narrow face) of
\(18.0\times10^{4}~\text {N}.\) The lower edge is riveted to the floor. The displacement of the upper edge is:
1.
\(30~\mu \text m\)
2.
\(48~\mu \text m\)
3.
\(16~\mu \text m\)
4.
\(64~\mu \text m\)
2. An equilateral triangular prism has three forces,
\(F\) each, acting normal to its rectangular faces: the forces being uniformly distributed over each face. The area of each face is
\(A.\) The coordinate axes
\(x,y\) are taken parallel to
\(BC\) & perpendicular to
\(BC\text-\) along the triangular face. Let the Young's modulus of the material of the prism be
\(Y\) & the Poisson's ratio be
\(\sigma.\) The strain along the
\(y\text-\)direction is:

1.
\(\dfrac{F}{AY}\)
2.
\(\dfrac{F}{2AY}\)
3.
\(\dfrac{F}{AY}(1-\sigma)\)
4.
\(\dfrac{F}{2AY}(1-\sigma)\)
3. A large beam sits vertically as shown in the figure. The beam has length
\(L,\) cross-sectional area
\(A,\) and the density of its material is
\(\rho.\) The compressive stress, in the middle of the beam, is: (take acceleration due to gravity as
\(g\))

| 1. |
\(\rho Lg\) |
2. |
\(\Large\frac{\rho Lg}{2}\) |
| 3. |
\(\Large\frac{\rho Lg}{4}\) |
4. |
\(2\rho Lg\) |
4. The density of ocean water varies with depth. This is due to:
1. elasticity
2. viscosity
3. surface tension
4. all of the above
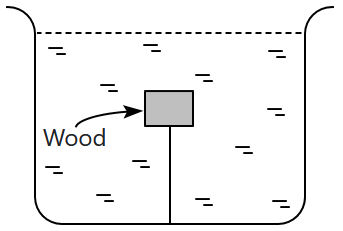
5. A block of wood is held under water by means of a thread attached to the bottom. The tension in the thread is
\(T_0.\) If the volume of the block is
\(V_0\) and its density is
\(\rho_0,\) then the force of buoyancy on the block is:
| 1. |
\(T_0\) |
2. |
\(\rho_0V_0g+T_0\) |
| 3. |
\(\rho_0V_0g-T_0\) |
4. |
\(T_0-\rho_0V_0g\) |
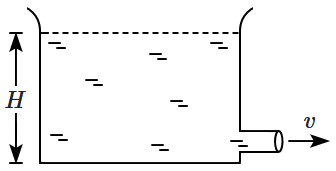
6. A water tank contains water up to a height
\(H.\) When a small pipe is opened at the bottom, water flows out at a speed
\(v.\) A graph of
\(v\) versus
\(H\) is:
1. a straight line
2. a circular arc
3. an ellipse
4. a parabola
7. The dimensions of the quantity
\(\Large\frac{\eta}{\rho}\) where
\(\eta\) is the viscosity and
\(\rho\) is the density are:
| 1. |
\(\left [ \dfrac{L}{T} \right ]\) |
2. |
\(\left [ \dfrac{L^2}{T} \right ]\) |
| 3. |
\(\left [ \dfrac{L}{T^2} \right ]\) |
4. |
\(\left [ \dfrac{L^3}{T^2} \right ]\) |
8. A small thin tube is connected to two soap bubbles, one of radius
\(R\) and the other radius
\(r\) — so that the air in the two bubbles can flow through the tube. Then, air will flow:
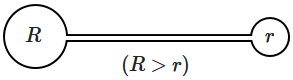
| 1. |
from the larger bubble to the smaller bubble, until the two are of equal size. |
| 2. |
from the large bubble to the smaller bubble initially, and the smaller one becomes larger; then the flow is reversed. |
| 3. |
from the smaller bubble to the larger one until the smaller bubble becomes very small. |
| 4. |
from the larger to the smaller bubble and it bursts the smaller bubble. |
9. A small spherical ball of radius \(0.1~\text{mm}\) and density \(10^{4}~\text{kg-m}^{-3}\) falls freely under gravity through a distance of \(h\) before entering a tank of water. If after entering the water, the velocity of the ball does not change and it continues to fall with the same constant velocity inside the water, then the value of \(h\) will be:
(given \(g=10~\text{m/s}^2,\) the viscosity of water \(=1.0\times10^{-5}~\text{N-sm}^{-2}\) )
1. \(15~\text m\)
2. \(25~\text m\)
3. \(20~\text m\)
4. \(10~\text m\)
10. Given below are two statements:
| Assertion (A): |
Insects are observed to walk on the surface of water. |
| Reason (R): |
This is due to the viscous force of water acting on the insect's legs. |
| 1. |
Both (A) and (R) are True and (R) is the correct explanation of (A). |
| 2. |
Both (A) and (R) are True but (R) is not the correct explanation of (A). |
| 3. |
(A) is True but (R) is False. |
| 4. |
(A) is False but (R) is True. |
11. Bernoulli's equation in fluid flow can be derived by using:
| 1. |
Conservation of momentum |
| 2. |
Conservation of angular momentum |
| 3. |
Work-energy theorem |
| 4. |
Torricelli's theorem |
12. A glass vessel having a coefficient of linear expansion \(\alpha\) is filled with a liquid. When the temperature of the vessel is raised, it is observed that the mass of the liquid filling the vessel remains unchanged. The coefficient of volume expansion of the liquid is:
1. \(\alpha\)
2. \(2\alpha\)
3. \(3\alpha\)
4. \(\dfrac\alpha3\)
13. On a cold winter day, the atmospheric temperature is constant and below freezing. A large lake begins to freeze uniformly from the surface downward, the thickness of ice being initially \(1~\text{cm}.\) When the thickness of ice becomes \(2~\text{cm},\) the rate of freezing (i.e., the rate of increase in thickness of ice) becomes, relative to its initial rate:
1. \(\dfrac12\)
2. \(\dfrac{1}{\sqrt2}\)
3. \(2\)
4. \(\sqrt2\)
14. The temperature \(\theta\) at the junction of two insulating sheets, having thermal resistances \(R_1 \) and \(R_2\) as well as top and bottom temperatures \(\theta_1\) and \(\theta\) (as shown in the figure) is given by :

1. \( \dfrac{\theta_2 R_2-\theta_1 R_1}{R_2-R_1} \)
2. \( \dfrac{\theta_1 R_2-\theta_2 R_1}{R_2-R_1} \)
3. \( \dfrac{\theta_1 R_2+\theta_2 R_1}{R_1+R_2} \)
4. \( \dfrac{\theta_1 R_1+\theta_2 R_2}{R_1+R_2} \)
15. For an ideal gas undergoing expansion or compression, we define the mechanical work done by:
\(dW=pdV.\)
A quantity
\(X\) is defined as follows:
\(dX=\dfrac{dW}{T},\) where
\(T\) is the absolute temperature.
Then, which of the following, is correct?
| 1. |
\(X\) depends on the process. |
| 2. |
\(X\) is independent of the process, but depends on \(p,V\) & \(T.\) |
| 3. |
\(X\) is independent of the process but depends only on \(p,V.\) |
| 4. |
\(X\) is independent of the process but depends only on \(V.\) |
16. During an experiment, an ideal gas is observed to obey the law: \(PV^3= \text{constant}\), as the process is conducted. If the volume of the gas doubles during this process, the absolute temperature of the gas changes from \(T\) to:
1. \(2T\)
2. \(4T\)
3. \(\dfrac T 2\)
4. \(\dfrac T 4\)
17. What is the molar-specific heat \((C_V)\) of a \(1:2\) molar mixture of monatomic & diatomic ideal gases?
1. \(\dfrac{11}{6}R\)
2. \(\dfrac{13}{6}R\)
3. \(5R\)
4. \(\dfrac{17}{6}R\)
18. \(n\) moles of an ideal gas with constant volume heat capacity \(C_V\) undergo an isobaric expansion by a certain volume. The ratio of the work done in the process, to the heat supplied is:
1. \( \dfrac{n R}{C_V+n R} \)
2. \( \dfrac{n R}{C_V-n R} \)
3. \( \dfrac{4 n R}{C_V+n R} \)
4. \( \dfrac{4 n R}{C_V-n R}\)
19. A gas at initial temperature \(T\) undergoes sudden expansion from volume \(V\) to \(2V.\) Then,
| 1. |
the process is adiabatic. |
| 2. |
the process is isothermal. |
| 3. |
the work done in this process is zero. |
| 4. |
the entropy in the process does not change. |
20. Graphs (drawn to the same scale) showing the variation of pressure with volume for a certain gas undergoing four different cyclic processes
\(\mathrm{A},\) \(\mathrm{B},\) \(\mathrm{C}\) and
\(\mathrm{D}\) are given below. Among these processes, the one in which the gas does the most work is:
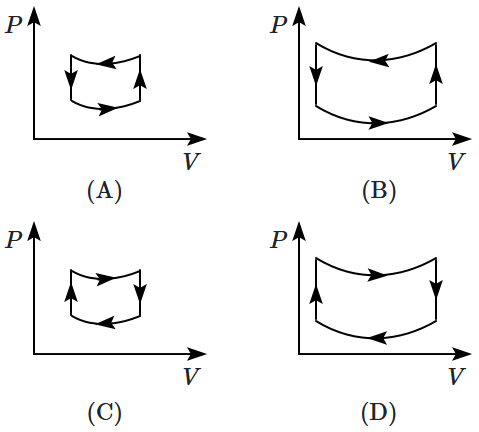
| 1. |
\(\mathrm{A}\) |
2. |
\(\mathrm{B}\) |
| 3. |
\(\mathrm{C}\) |
4. |
\(\mathrm{D}\) |
21. A monatomic ideal gas changes from an initial state \(\left(P_{i,} {V}_i, T_{i}, n_{i}\right)\) to a final state \(\left(P_{f}, V_{f}, T_{f}, n_{f}\right) {P}_{i}<{P}_{f}, {V}_{i}={V}_{f}, {T}_{i}<{T}_{f}\) and \(n_{i}=n_{f} .\) Which of the following gives the change in the entropy of the gas?
1. \(\dfrac{3}{2} n R \mathrm{ln} \left(\dfrac{T_{f}}{T_{i}}\right)\)
2. \(\dfrac{3}{2} n R \mathrm {ln} \left(\dfrac{T_{i}}{T_{f}}\right)\)
3. \(\dfrac{5}{2} n R \mathrm{ln} \left(\dfrac{T_{f}}{T_{i}}\right)\)
4. \(\dfrac{5}{3} n R \mathrm{ln} \left(\dfrac{T_{f}}{T_{i}}\right)\)
22. During a reversible adiabatic process, a monoatomic ideal gas follows the equation (\(P,V,T\) represent pressure, volume and temperature of the gas):
1. \(PV\) = constant
2. \(PV^{2/3}\) = constant
3. \(PV^{1.4}\) = constant
4. \(PV^{5/3}\) = constant
23. Which one of the following schematic graphs best represents the variation of
\(PV\) (in joules) versus
\(T\) (in kelvin) of one mole of an ideal gas? (The dotted line represents
\(PV=T\)).
24. The energy of a gas molecule in a gas at a given temperature
\(T~(\text{K})\) is calculated based on the kinetic theory of gases. Match
Column-I with
Column-II.
|
Column-I |
|
Column-II |
| (A) |
mean kinetic energy per mole of diatomic gas |
(P) |
\(\dfrac{3}{2}k_BT\) |
| (B) |
mean transitional kinetic energy per molecule of a gas |
(Q) |
\(\dfrac{3}{2}RT\) |
| (C) |
mean translational kinetic energy per mole of an ideal gas |
(R) |
\(\dfrac{5}{2}RT\) |
| (D) |
mean rotational kinetic energy per molecule of diatomic gas |
(S) |
\(k_BT\) |
| 1. |
A(P), B(R), C(S), D(Q) |
| 2. |
A(R), B(Q), C(P), D(S) |
| 3. |
A(R), B(S), C(Q), D(P) |
| 4. |
A(R), B(P), C(Q), D(S) |
25. To raise the temperature of a certain mass of gas by \(50^\circ\text{C}\) at a constant pressure, \(160\) calories of heat is required. When the same mass of gas is cooled by \(100^\circ\text{C}\) at constant volume, \(240\) calories of heat is released. How many degrees of freedom does each molecule of this gas have (assume the gas to be ideal)?
1. \(2\)
2. \(5\)
3. \(6\)
4. \(3\)
26. Given below are two statements:
| Assertion (A): |
The molar heat capacity of the gas can have any value from \(-\infty\) to \(\infty\). |
| Reason (R): |
The molar heat capacity of the gas for the isothermal process is \(\infty\). |
| 1. |
Both (A) and (R) are True and (R) is the correct explanation of (A). |
| 2. |
Both (A) and (R) are True but (R) is not the correct explanation of (A). |
| 3. |
(A) is True but (R) is False. |
| 4. |
Both (A) and (R) are False. |
27. A simple pendulum is taken into an elevator that is moving up with an acceleration equal to \(g.\) If its time period was \(T\) before, the new time period will be:
1. \(2T\)
2. \(\sqrt2T\)
3. \(\dfrac{T}{2}\)
4. \(\dfrac{T}{\sqrt2}\)
28. If a simple pendulum be suspended in an elevator which is moving upward, its time period is found to decrease by \(2\%.\) The acceleration of the elevator is (in magnitude):
1. \(2\%\) of \(g\)
2. \(1\%\) of \(g\)
3. \(4\%\) of \(g\)
4. \(102\%\) of \(g\)
29. The total energy of oscillation, of a particle executing SHM, is proportional to \(A^{\lambda};\) where \(A\) is the amplitude of oscillation and \(\lambda\) is a constant. Then, \(\lambda\) equals:
1. \(2\)
2. \(4\)
3. \(-2\)
4. \(-4\)
30. Two identical blocks are connected by an ideal spring and the system is allowed to oscillate, when undergoing horizontal displacements in opposite directions, with the centre-of-mass at rest.
\(O\) is the mid-point of the spring,
\(A\) is left end point,
\(B\) is the right end-point. The motion of
\(A\) is described by:
\(x_A = A_0 \sin \omega t\) (displacement is taken to be positive rightward).
Call the mid-point of
\(O\) and
\(B\) as
\(C\) and its
\(x\text-\)coordinate as
\(x_C.\) Then, the motion of the point
\(C\) of the spring is described by:

1.
\(x_{C}=A_{0} \sin \left(\omega t+\dfrac{\pi}{2}\right)\)
2.
\(x_{C}=\dfrac{A_{0}}{2} \sin \omega t\)
3.
\(x_{C}=\dfrac{A_{0}}{2} \sin \left(\omega t+\dfrac{\pi}{2}\right)\)
4.
\(x_{C}=\dfrac{A_{0}}{2} \sin (\omega t+\pi)\)
31. If two identical springs of stiffness \(k\) (each) are combined end-to-end, the resulting spring has a stiffness:
1. \(k\)
2. \(2k\)
3. \(\Large\frac k2\)
4. zero
32. A graph is plotted with the \(x \text-\)axis representing the position and the \(y\text-\)axis representing the velocity of a particle undergoing SHM along a straight line. The shape of the graph is:
| 1. |
a straight line with a positive slope |
| 2. |
a straight line with a negative slope |
| 3. |
a circle |
| 4. |
an ellipse |
33. The maximum speed and acceleration of a particle undergoing SHM are \(v_0\) and \(a_0,\) respectively. The time period of the SHM is:
1. \(\dfrac{2\pi v_0}{a_0}\)
2. \(\dfrac{2\pi a_0}{v_0}\)
3. \(\dfrac{v_0}{a_0}\)
4. \(\dfrac{2v_0}{a_0}\)
34. A block is suspended from a spring and allowed to oscillate vertically, giving a time period
\(T.\) If the block is suspended from the same spring, the elongation produced will be:
| 1. |
\(\dfrac12gT^2\) |
2. |
\(\dfrac14gT^2\) |
| 3. |
\(\dfrac{1}{2\pi}gT^2\) |
4. |
\(\dfrac{1}{4\pi^2}gT^2\) |
Physics - Section B
35. A heavy uniform rope hanging under its own weight from the ceiling of a room, can propagate small disturbances along its length as it is under tension. Let the mass per unit length of the rope be
\(\mu,\) and its total length
\(L.\)
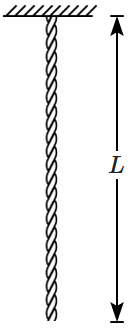
The tension in the rope, at a point at a distance
\(x\) above the lowest point, is:
1.
\(\mu gL\)
2.
\(\mu g(L-x)\)
3.
\(\mu gx\)
4.
\(\dfrac{\mu gx}{2}\)
36. The two lowest notes on the piano are \({A_0}\) \((27.5~\text{Hz})\) and \({A}{\#}_{0}\) \((29.1~\text{Hz}).\) If you play the notes simultaneously, the resulting sound seems to turn off and on and off and on. How much time exists between the successive "on" \(\text s?\)
1. \(0.6~\text s\)
2. \(1.6~\text s\)
3. \(28.3~\text s\)
4. \(56.6~\text s\)
37. Planet Jupiter has an atmosphere mainly of methane at \(-130^\circ \text{C}.\) The velocity of sound on this planet assuming \(\gamma \left ( \dfrac{C_{P}}{C_{V}} \right )\) for mixture to be \(1.3\) is:
(gas constant \(R=8.3~\text{J/mol-K},\) molecular mass of methane \(=16~\text{gm}\))
1. \(311~\text{m/s} \)
2. \(10~\text{m/s}\)
3. \(275~\text{m/s}\)
4. \(350~\text{m/s}\)
38. Two vibrating tuning forks producing progressive waves given by;
\(y_1=4\sin(500 \pi t-k_1x),\) \(y_2=2\sin(506\pi t-k_2x)\) are held near the ear of a person. The person will hear:
1. \(9~\text{beats/s}\)
2. \(6~\text{beats/s}\)
3. \(3~\text{beats/s}\)
4. \(2~\text{beats/s}\)
39. The separation between a node and the next antinode in a vibrating air column is \(20\) cm. The speed of sound is \(320\) m/s. The frequency of sound is:
1. \(128\) Hz
2. \(256\) Hz
3. \(400\) Hz
4. \(800\) Hz
40. When two tuning forks with nearly equal frequencies (say:
\(100~\text{Hz}\) and
\(102~\text{Hz}\)) are sounded together,
| 1. |
Beats of frequency \(2~\text{Hz}\) are heard |
| 2. |
Beats of frequency \(101~\text{Hz}\) are heard |
| 3. |
Echo of frequency \(202~\text{Hz}\) is heard |
| 4. |
Standing waves of frequency \(202~\text{Hz}\) are formed |
41. Two concentric spherical shells of radii
\(r_1\) &
\(r_2,\) made of material having emissivity
\(e_1\) &
\(e_2\) are at absolute temperatures
\(T_1\) &
\(T_2,\) respectively: the inner sphere being maintained at a temperature
\(T_1\) by means of a source of heat within. Take Stefan's constant to be
\(\sigma;\) Areas
\(A_1=4\pi r^2_1\) &
\(A_2=4\pi r^2_2.\)

Assume that
\(e_1=e_2=1.\) What is the rate of radiation from the inner sphere, falling on the outer sphere?
1.
\(\sigma A_1T_1^4\)
2.
\(\sigma A_1T_1^4-\sigma A_2T_2^4\)
3.
\(\sigma A_1\left(T_1^4-T^4_2\right)\)
4.
\(\sigma A_2T_1^4\)
42. Two concentric spherical shells of radii
\(r_1\) &
\(r_2,\) made of material having emissivity
\(e_1\) &
\(e_2\) are at absolute temperatures
\(T_1\) &
\(T_2,\) respectively: the inner sphere being maintained at a temperature
\(T_1\) by means of a source of heat within. Take Stefan's constant to be
\(\sigma;\) Areas
\(A_1=4\pi r^2_1\) &
\(A_2=4\pi r^2_2.\)

Assume that
\(e_1=e_2=1.\) What is the rate of radiation from the outer sphere, falling on the inner sphere?
1.
\(\sigma A_2T_2^4\)
2.
\(\sigma A_2T_2^4-\sigma A_1T_1^4\)
3.
\(\sigma A_1T_2^4\)
4.
\(\sigma A_2T_1^4\)
43. Two concentric spherical shells of radii
\(r_1\) &
\(r_2,\) made of material having emissivity
\(e_1\) &
\(e_2\) are at absolute temperatures
\(T_1\) &
\(T_2,\) respectively: the inner sphere being maintained at a temperature
\(T_1\) by means of a source of heat within. Take Stefan's constant to be
\(\sigma;\) Areas
\(A_1=4\pi r^2_1\) &
\(A_2=4\pi r^2_2.\)

Assume that
\(e_1=e_2=1.\) What is the rate at which radiation from the outer sphere directly falls on the outer sphere, itself?
1. zero
2.
\(\sigma A_2T_2^4-\sigma A_1T_1^4\)
3.
\(\sigma A_1T_2^4\)
4.
\(\sigma \left(A_2-A_1\right)T_2^4\)
44. Two concentric spherical shells of radii
\(r_1\) &
\(r_2,\) made of material having emissivity
\(e_1\) &
\(e_2\) are at absolute temperatures
\(T_1\) &
\(T_2,\) respectively: the inner sphere being maintained at a temperature
\(T_1\) by means of a source of heat within. Take Stefan's constant to be
\(\sigma;\) Areas
\(A_1=4\pi r^2_1\) &
\(A_2=4\pi r^2_2.\)

Let
\(e_1\neq1\) and
\(e_2=1.\) What is the rate of radiation from the inner sphere, falling on the outer sphere?
1.
\(e_1\sigma A_1T_1^4\)
2.
\(e_1\sigma A_1T_1^4-\sigma A_2T_2^4\)
3.
\(e_1\sigma\left(A_1T_1^4-A_2T_2^4\right)\)
4.
\(e_1\sigma A_1\left(T_1^4-T_2^4\right)\)
45. Two concentric spherical shells of radii
\(r_1\) &
\(r_2,\) made of material having emissivity
\(e_1\) &
\(e_2\) are at absolute temperatures
\(T_1\) &
\(T_2,\) respectively: the inner sphere being maintained at a temperature
\(T_1\) by means of a source of heat within. Take Stefan's constant to be
\(\sigma;\) Areas
\(A_1=4\pi r^2_1\) &
\(A_2=4\pi r^2_2.\)

Let
\(e_1\neq1\) and
\(e_2=1.\) What is the rate of radiation from the outer sphere, falling on the inner sphere?
1.
\(\sigma A_2T_2^4\)
2.
\(e_1\sigma A_2T_2^4\)
3.
\(e_1\sigma A_1T_2^4\)
4.
\(\sigma A_1T_2^4\)
46. Two concentric spherical shells of radii
\(r_1\) &
\(r_2,\) made of material having emissivity
\(e_1\) &
\(e_2\) are at absolute temperatures
\(T_1\) &
\(T_2,\) respectively: the inner sphere being maintained at a temperature
\(T_1\) by means of a source of heat within. Take Stefan's constant to be
\(\sigma;\) Areas
\(A_1=4\pi r^2_1\) &
\(A_2=4\pi r^2_2.\)

Let
\(e_1\neq1\) and
\(e_2\neq1.\) What is the rate of radiation emerging from the outer sphere?
1.
\(\sigma A_2T_2^4\)
2.
\((1+e_1)\sigma A_2T_2^4\)
3.
\((A_2+e_1A_1)\sigma T_2^4\)
4.
\(2e_2\sigma A_2T_2^4\)
*If above link doesn't work, please go to test link from where you got the pdf and fill OMR from there
CLICK HERE to get FREE ACCESS for 2 days of ANY NEETprep course