A thin disc of mass 9 M and radius R from which a disc of radius R/3 is cut is shown in fig. Then moment of inertia of the remaining disc about O, perpendicular to the plane of disc is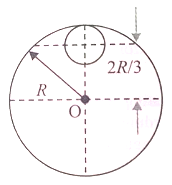
A uniform thin bar of mass 6 m and length 12 L is bent to make a regular hexagon. Its moment of inertia about an axis passing through the centre of mass and perpendicular to the plane of the hexagon is
A solid sphere is rolling without slipping, its translational K.E. is 50 J then its rotational K.E. is :
1. 20 J
2. 50 J
3. 70 J
4. 40 J
A thin uniforming circular disc of mass M and radius R is rotating in a horizontal plane about an axis passing through its centre and perpendicular to the plane with angular velocity . Another disc of same mass but half the radius is gently placed over it coaxially. The angular speed of the composite disc will be
A cord is wound around the circumference of wheel of radius r. The axis of the wheel is horizontal and the moment of inertia about it is I. A weight mg is attached to the cord at the end. The weight falls from rest. After falling through a distance h, the angular velocity of the wheel will be
A small object of uniform density rolls up a rough curved surface with an initial velocity v. It reaches upto a maximum height of 3 v/4 g with respect to the initial position. The object is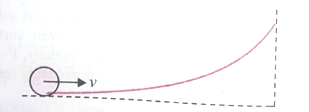
1. ring
2. solid sphere
3. hollow sphere
4. disc
A sphere of mass M rolls without slipping on an inclined plane of inclination . What should be the minimum coefficient of friction, so that the sphere rolls down without slipping?
A mass M is supported by a massless string wound round uniform cylinder of mass M and radius R. On releasing the mass from rest, it will fall with acceleration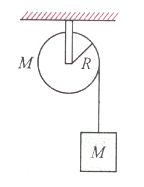
1. g
2. g/2
3. g/3
4. 2 g/3
A heavy ball is thrown on a rough horizontal surface in such a way that it slides with a speed initially without rolling. It will roll without sliding when its speed falls to
A solid ball of radius r rolls inside a hemispherical shell of radius R. It is released from rest from point A as shown in fig. The angular velocity of centre of the ball in position B about the centre of the shell is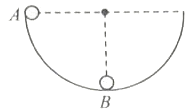
The speed of a homogeneous solid sphere after rolling down an inclined plane of vertical height h from rest without sliding is
In the fig, the plank is being pulled to the right with a constant speed v. If the cylinder does not slip, then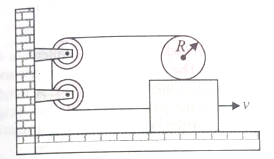
1. the speed of the centre of mass of the cylinder is 2 v
2. the speed of the centre of mass of the cylinder is v
3. the angular velocity of the cylinder is v/R
4. the angular velocity of the cylinder is zero
The minimum value of F for which the cube () begins to topple about an edge is.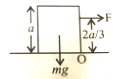
A thin circular ring of mass M and radius r rotating about an axis passing through its centre and perpendicular to its plane with a constant angular velocity . Two objects, each of mass m are attached gently to the opposite ends of a diameter of the ring. The ring now rotates with angular velocity
A uniform rod of length l is free to rotate in a verticle plane about a fixed horizontal axis through O. The rod is allowed to rotate from its unstable verticle position. Then the angular velocity of the rod when it has turned through an angle is :
From the circular disc of radius R and mass M, a concentric circular disc of small radius r is cut and removed, the mass of which is m. The moment of inertia of the angular disc remaining, about its axis perpendicular to the plane and passing through the centre of mass will be
A thin wire of length L and uniform density is bent into a circular loop with centre at O as shown. The moment of inertia of the loop about the axis xx' is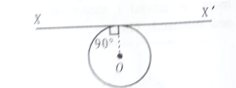
A string of negligible thickness is wrapped several times around a cylinder kept on a rough horizontal surface. A man standing at a distance l from the cylinder holds one end of the string and pulls the cylinder towards him. There is no slipping anywhere. The length of the string that passed through the hand of the man while the cylinder reaches his hands is-[Assume radius of the cylinder is negligible compared to length 'l' of string]
| 1. | l | 2. | 2l |
| 3. | 3l | 4. | 4l |
A T shaped object with dimensions shown in the figure, is lying on a smooth floor. A force is applied at the point P parallel to AB, such that the object has only the translational motion without rotation. Find the location of P with respect to C.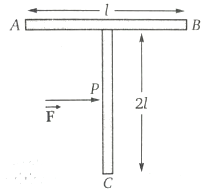
Four point masses, each of value m, are placed at the corners of a square ABCD of side l. The moment of inertia of this system about an axis passing through A and parallel to BD is
Moment of Inertia of the rod AB about the axis YY'