Two particles \(A\) and \(B,\) move with constant velocities \(\vec{v_1}\) and \(\vec{v_2}.\) At the initial moment their position vector are \(\vec {r_1}\) and \(\vec {r_2}\) respectively. The conditions for particles \(A\) and \(B\) for their collision to happen will be:
| 1. | \(\vec{r_{1 }} . \vec{v_{1}} = \vec{r_{2 }} . \vec{v_{2}}\) | 2. | \(\vec{r_{1}} \times\vec{v_{1}} = \vec{r_{2}} \times \vec {v_{2}}\) |
| 3. | \(\vec{r_{1}}-\vec{r_{2}}=\vec{v_{1}} - \vec{v_{2}}\) | 4. | \(\frac{\vec{r_{1}} - \vec{r_{2}}}{\left|\vec{r_{1}} - \vec{r_{2}}\right|} = \frac{\vec{v_{2}} - \vec{v_{1}}}{\left|\vec{v_{2}} - \vec{v_{1}}\right|}\) |
A particle of mass 'm' is moving in circular path of constant radius 'r' such that centripetal acceleration is varying with time 't' as where K is a constant. The power delivered to the particle by the force acting on it is
If and represent the work done in moving a particle from A to B along three different paths 1, 2 and 3 respectively (as shown) in the gravitational field of a point mass m, find the correct relation between and .
A stone is tied to a string of length and is whirled in a vertical circle with the other end of the string as the centre. At a certain instant of time, the stone is at its lowest position and has speed u. The magnitude of the change in velocity as it reaches a position where the string is horizontal (g being acceleration due to gravity) is
The given plot shows the variation of U, the potential energy of interaction between two particles with the distance separating them, r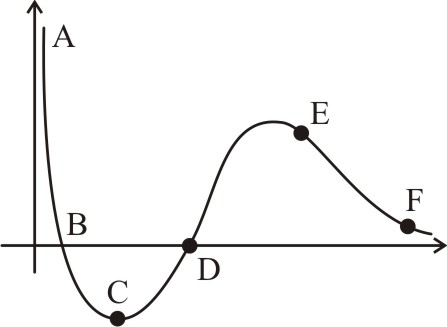
1. B and D are equilibrium points
2. C is a point of stable equlibrium
3. The force of interaction between the two particles is attractive between points C and D and repulsive between points D and E on the curve.
4. The force of interaction between the particles is attractive between points E and F on the curve.
A particle is moving in a region where the potential U is given by U = . The force acting on the particle is
A force , acts on a particle moving in the x-y plane. Starting from the origin, the particle is taken along the positive x-axis to the point (, 0) and is then taken parallel to the y-axis to the point . The total work done by the force is
A box is moved along a straight line by a machine delivering constant power. The distance moved by the body in time t is proportional to
A motor is used to deliver water at a certain rate through a given horizontal pipe. To deliver n-times the water through the same pipe in the same time the power of the motor must be increased as follows
1. n times
2. n times
3. n times
4. n times
The potential energy of a \(1 ~\text{kg}\) particle free to move along the \(x\text-\)axis is given by \(U(x)=\left(\frac {x^4}{ 4}-\frac {x^2}{ 2}\right)~\text J.\) The total mechanical energy of the particle is \(2~\text J.\) Then the maximum speed (in \(\text{ms}^{-1}\)) will be:
1. \(\dfrac{3}{\sqrt{2}} \)
2. \(\sqrt{2}\)
3. \(\dfrac{1}{\sqrt{2}}\)
4. \(2\)
A small body of mass m slides without friction from the top of a hemisphere of radius r. At what height will the body be detached from the center of the hemisphere
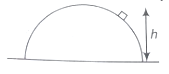
A ball is dropped on to a smooth horizontal plane from certain height h. Assuming the coefficient of restitution of impact is e
The total distance covered by the ball till it stops
1.
2.
3.
4. None
Find the potential energy stored in the springs in equilibrium. [in 10]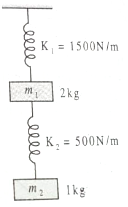
A ball moving with a speed of 9 m/s strikes an identical stationary ball such that after the collision the direction of each ball makes an angle of 30 with the original line of motion. Find the speed of each ball after the collision.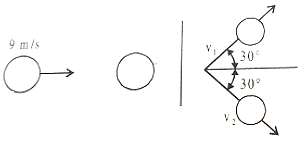
1. 5 m/s
2. 4 m/s
3. 6 m/s
4. 10 m/s
If kinetic energy of a body is increased by 300% then percentage change in momentum will be
1. 100%
2. 150%
3. 265%
4. 73.2%
A small object A slide down with zero initial velocity from position (1) shown in the figure. Height of position (1) is H. At position (2) track is horizontal and its height from ground is h. After position (2) particle travel in air and lets at a distance on the ground as shown.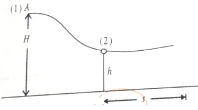
Value of h for s to maximum
A ball is thrown towards a floor with speed u. The coefficient of restitution between floor and ball is ''e''. The speed with which ball rebounds is: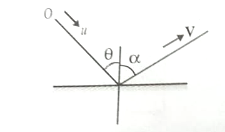
A pendulum consists of a wooden bob of mass m and length l. A bullet of is fired towards the pendulum with a speed . The bullet emerges out of bob with a speed and the bob just completes motion along a verticle circle, then is:
A block of mass m is taken from A to B under the action of a constant force F. Work done by this force is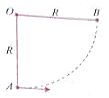
Consider the system shown in the figure. Coefficient of friction between the block and table is = 0.5. The system is released from rest. Find the work done by friction, from the time system starts moving to the time when the speed of block is 10 m/s. (m = 1 kg)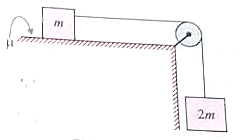
1. -10 J
2. -20 J
3. -30 J
4. -50 J
Velocity-time graph of a particle of mass 2 kg moving in a straight line is a shown in figure. Work done by all the forces on the particle from t = 0 to t = 2 sec is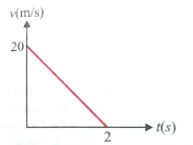
1. 400 J
2. -400 J
3. -200 J
4. 200 j
A block of mass M slides along the sides of a bowl as shown in fig. The walls of the bowl are frictionless and the base has coefficient of friction 0.2. If the block is released from the top of the side, which is 1.5 m high, where will the block come to rest? Given that the length of the base is 15 m.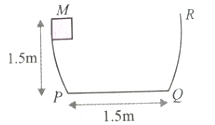
1. 1 m from P
2. Mid point of PQ
3. 2 m from P
4. at Q
A uniform chain of length L and mass M is lying on a smooth table and one third of its length is hanging vertically down over the edge of the table. if g is acceleration due to gravity, the work required to pull the hanging part on the table is
1. MgL
2. MgL/3
3. MgL/9
4. MgL/18