The following four wires length L and radius r are made of the same material. Which of these will have the largest extension, when the same tension is applied?
1. L = 400 cm, r = 0.8 mm
2. L = 300 cm, r = 0.6 mm
3. L = 200 cm, r = 0.4 mm
4. L = 100 cm, r = 0.2 mm
A solid sphere of radius R made up of a material of bulk modulus K is surrounded by a liquid in a cylindrical container. A massless piston of area A floats on the surface of the liquid. When a mass M is placed on the piston to compress the liquid, the fractional change in the radius of the sphere is:
1. Mg/AK
2. Mg/3AK
3. 3Mg/AK
4. Mg/2AK
A copper rod of length L and radius is suspended from the ceiling by one of its ends. What will be the elongation of the rod due to its own weight when and Y are the density and Young's modulus of the copper respectively?
1.
2.
3.
4.
Two wires of length l, radius r and length 2l, radius 2r respectively having same Young's modulus are hung with a weight mg. Net elongation is
1.
2.
3.
4.
A metallic ring of radius r and cross-sectional area A is fitted into a wooden circular disc of radius R (R>r). If Young's modulus of the material of the ring is Y, the force with which the metal ring expands is
1.
2.
3.
4.
A rod of length I and radius r is joined to a rod of length 1/2 and radius r/2 of the same material. The free end of the small rod is fixed to a rigid base and the free end of the larger rod is given a twist of °, the twist angle at the joint will be
1. /4
2. /5
3. 5/6
4. 8/9
A wire of natural length 1, Young's modulus Y, and area of cross-section A are extended by x. Then the energy stored in the wire is given by
1.
2.
3.
4.
There is no change in the volume of a wire due in the change in its length on stretching. The Poisson's ratio of the material of the wire is
1. +0.50
2. -0.50
3. +0.25
4. -0.25
Two wires of lengths and cross-sectional areas \(L_1, L_2~\text{and}~A_1,A_2\) respectively, are joined together and suspended from a support. The sphere of mass \(M\) is suspended from the other end. The Young's modulus of two wires are \(Y_1~\text{and}~Y_2\) respectively. If the deformation in the wire is \(Mg\left(\frac{\alpha_1 L_2 + Y_2A_2L_1}{\alpha_1Y_2A_2}\right)\) then \(\alpha_1\) is:
1. \(A_1Y_2\)
2. \(A_2Y_1\)
3. \(A_1Y_1\)
4. \(A_2Y_2\)
A bar of unknown mass and length of 2 m is suspended by two wires of same length L and cross-sectional areas of 0.1 and 0.19 and elongation of 0.19 L and 0.20 L respectively under the action of a weight hanging at a distance of 4/3 m on the bar from end B. The length of the bar is comparable with L. Which of the following terms is equal for two wires
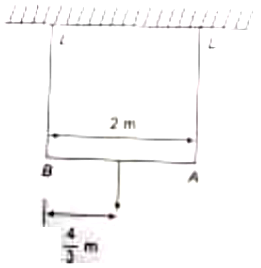
1. Stress
2. Strain
3. Young's modulus
4. None of the above
The product of Young's modulus of the material of the wire with its cross-sectional areas is equal to its length. Find the parameters representing x and y axes of the curve shown in figure
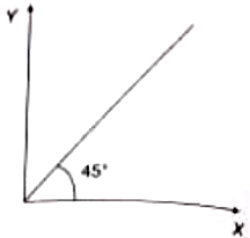
1. Load and increase in length
2. Stress and strain
3. Young's modulus and stress
4. Young's modulus and strain
The length of wire OE is divided into five equal parts OA, AB, BC, CD, and DE. The wire is hanging from E and its length is given by .where o is the breaking stress and p is the density of the material of the wire. Find the point at which wire will break.
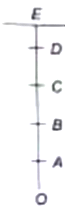
1. A
2. B
3. C
4. D
A mass m is hanging from a wire of cross-sectional area A and length I. Y is young's modulus of wire. An external force F is applied on the wire which is slowly further pulled down by x from its equilibrium position. Find the work done by the force F the wire exerts on the mass.
1.
2.
3.
4.
The pressure of a medium is changed from 1.01 x Pa to 1.165 x and change in volume is 10% keeping temperature constant. The Bulk modulus of the medium is
1. 1.55 X Pa
2. 205 x Pa
3. 107.4 x Pa
4. 83.7 x Pa
For a given material, Young's modulus is 2.4 times that of rigidity modulus. Its Poisson's ratio is
1. 2.4
2. 1.2
3. 0.4
4. 0.2
The length of an elastic spring is a meter when a force of 4 N is applied and b meters when 5 N is applied. Then the length of the spring when the 9 N force is applied is
1. a + b
2. 9b - 9a
3. 5b - 4a
4. 4a - 5b
Young's modulus of perfectly rigid body material is
1. Infinite
2. Zero
3.
4.
The hollow shaft is...... than a solid shaft of the same mass, material, and length
1. Less stiff
2. More stiff
3. Equally stiff
4. None of these