A 10 g piece of iron (C = 0.45 J/g°C) at 100 °C is dropped into 25 g of water (C = 4.2 J/g°C) at 27°C. Find the temperature of the iron and water system at thermal equilibrium.
1. 30 °C
2. 33 °C
3. 40 °C
4. None of these
2 mole of zinc is dissolved at HCI at .
The work done in open vessel is:
1. -2.477 KJ
2. -4.955 KJ
3. 0.0489 KJ
4. None
A sample of an ideal gas is expanded 1 to 3 in a reversible process for which P = K, with K = 6 bar/m. Work done by the gas is
1. 5200 kJ
2. 15600 kJ
3. 52 kJ
4. 5267.6 kJ
An ideal gas is taken around the cycle ABCA as shown in P-V diagram. The network done during the cycle is equal to :
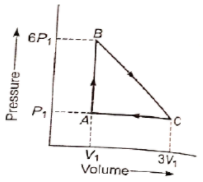
1. 12
2. 6
3. 5
4.
A gas expands against a variable pressure given by P = 20/V (where P in atm and V in L). During expansion from the volume of 1 liter to 10 liters, the gas undergoes a change in internal energy of 400 J. How much heat is absorbed by the gas during expansion?
1. 46 J
2. 4660 J
3. 5065.8 J
4. 4260 J
5 mole of an ideal gas expand isothermally and irreversibly from a pressure of 10 atm to 1 atm against a constant external pressure of 1 atm, at 300 K is:
1. -15.921 KJ
2. -11.224 KJ
3. -110.83 KL
4. None of these
One mole of a non-ideal gas undergoes a change of state from (1.0 atm, 3.0 L, 200 K) to (4.0 atm, 5.0 L, 250 K) with a change in internal energy (U) = 40 L-atm. The change in enthalpy of the process in L-atm:
1. 43
2. 57
3. 42
4. None of these
Consider the reaction at 300 K . What is AU for the combustion of 1.5 moles of benzene at 27°C
1. -3267.25 kJ
2. -4900.88 kJ
3. -4906.5 kJ
4. -3274.75 kJ
When two moles of an ideal gas ( = R) heated from 300 K to 600 K at constant pressure. The change in entropy of gas S is
1.
2. -
3.
4.
When one mole of an ideal gas is compressed to half of its initial volume and simultaneously heated to twice its initial temperature, the change in entropy of gas (S) is :
1. In 2
2. In 2
3. R In 2
4. ( = R) In 2
What is the change in entropy when 2.5 moles of water is heated from 27 °C to 87°C? Assume that the capacity is constant ()
1. 16.6 J/K
2. 9 J/K
3. 34.02 J/K
4. 1.89 J/K
At 25 °C, for the process (l) (g) is 8.6 kJ. The vapor pressure of water at this temperature is near:
1. 24 torr
2. 285 torr
3. 32.17 torr
4. 100 torr
The standard enthalpy of formation of gaseous at 298 K is -241.82 kJ/mol. Calculate at 373 K given the following values of the molar heat capacities at constant pressure:
; ; .
Assume that the heat capacities are independent of temperature :
1. -242.6 kJ/mol
2. -485.2 kJ/mol
3. -121.3 kJ/mol
4. -286.4 kJ/mol
Gasoline has an enthalpy of combustion 24000 kJ/gallon. When gasoline burns in an automobile engine, approximately 30% of the energy released is used to produce mechanical work. The remainder is lost as heat transfer to the engine's cooling system. As a start on estimating how much heat transfer is required, calculate what mass of water could be heated from 25 °C to 75 °C by the combustion of 1.0 gallons of gasoline in an automobile? (Given : C() = 4.18 J/g°C)
1. 34.45 kg
2. 80.383 kg
3. 22 kg
4. 224 kg
A 0.05 L sample of 0.2 M aqueous hydrochloric acid is added to 0.05 L of 0.2 M aqueous ammonia in a calorimeter. The heat capacity of the entire calorimeter system is 480 J/K. The temperature increase is 1.09 K. Calculate in kJ/mol for the following reaction:
1. -52.32
2. -61.1
3. -55.8
4. -58.2
Boron can undergo the following reactions with the given enthalpy changes: 2B(s)
Assume no other reactions are occurring. If in a container (operating at constant pressure) which is isolated from the surrounding, a mixture of H2(gas) and (gas) is passed over excess of B(s), then calculate the molar ratio () so that the temperature of the container does not change :
1. 15:3
2. 42:1
3. 1:42
4. 1:84