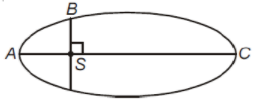
The kinetic energies of a planet in an elliptical orbit about the Sun, at positions A, B, and C are , respectively. AC is the major axis and SB is perpendicular to AC at the position of the Sun S as shown in the figure. Then
1.
2.
3.
4.
If the mass of the Sun were ten times smaller and the universal gravitational constant were ten times larger in magnitude, which of the following is not correct?
1. Raindrops will fall faster
2. Walking on the ground would become more difficult
3. g on the Earth will not change
4. Time period of a simple pendulum on the Earth would decrease
The acceleration due to gravity at a height 1 km above the earth is the same as at a depth d below the surface of the earth. Then
1. d = km
2. d = 1 km
3. d = km
4. d = 2 km
Two astronauts are floating in gravitational free space after having lost contact with their spaceship. The two will contact with their spaceship. Two will
1. Keep flotation at the same distance between them
2. Move towards each other
3. Move away from each other
4. Will become stationary
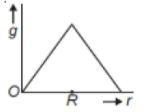
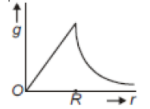
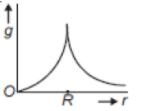
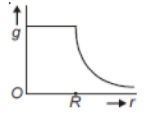
Starting from the center of the earth having radius R, the variation of g (acceleration due to gravity) is shown by
1. 
2. 
3. 
4. 
A satellite of mass m is orbiting the earth (of radius R) at a height h from its surface. The total energy of the satellite in terms of go, the value of acceleration due to gravity at the earth's surface, is
1.
2.
3.
4.
At what height from the surface of the earth, the gravitation potential and the value of g are respectively? Take the radius of earth as 6400 km
1. 2000 km
2. 2600 km
3. 1600 km
4. 1400 km
The ratio of escape velocity at earth () to the escape velocity at a planet () whose radius and mean density are twice as that of the earth is
1. 1:
2. 1:2
3. 1:2
4. 1:4
A satellite S is moving in an elliptical orbit around the earth. The mass of the satellite is very small compared to the mass of the earth. Then,
1. The acceleration of S always directed towards the centre of the earth.
2. The angular momentum of S about the centre of the earth changes in direction, but its magnitude remains constant
3. The total mechanical energy of S varies periodically with time
4. The linear momentum of S remains constant in magnitude
A remote-sensing satellite of earth revolves in a circular orbit at a height of 0.25 x m above the surface of the earth. If the earth's radius is 6.38 x m and g = 9.8 , then the orbital speed of the satellite is
1. 6.67 km
2. 7.76 km
3. 8.56 km
4. 9.13 km
Kepler's third law states that square of the period of revolution (T) of a planet around the sun, is proportional to the third power of average distance r between sun and planet, i.e., , here K is constant. If the masses of sun and planet are M and m respectively then as per Newton's law of gravitation force of attraction between them is F = , here G is gravitational constant. The relation between G and K is described as
1. K = 1/G
2. GK = 4
3. GMK = 4
4. K = G
A black hole is an object whose gravitational field is so strong that even light cannot escape from it. To what approximate radius would earth (mass = 5.98 x kg) have to be compressed to be a black hole?
1. m
2. m
3. m
4. 100 m
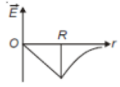
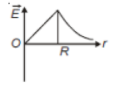
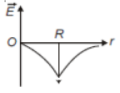
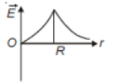
Dependence of intensity of gravitational field () of the earth with distance (r) from the centre of the earth is correctly represented by
1. 
2. 
3. 
4. 
A body of mass m is taken from the earth's surface to the height equal to twice the radius (R) of the earth. The change in potential energy of the body will be
1. mgr
2. 3 mg
3. mgr
4. mg2R
An infinite number of bodies, each of mass 2 kg are situated on the x-axis at distances 1 m, 2 m, 4 m, 8 m, ....., respectively, from the origin. The resulting gravitational potential due to this system at the origin will be
1. - G
2. - G
3. -4 G
4. -G