1. Which of the following pairs of physical quantities does not have the same dimensional formula?
| 1. |
work and torque |
| 2. |
angular momentum and Planck's constant |
| 3. |
tension and surface tension |
| 4. |
impulse and linear momentum |
2. A lift is coming from 8th floor and is just about to reach 4th floor. Taking ground floor as origin and positive direction upwards for all quantities, which one of the following is correct?
1. \(x<0, v<0, a>0 \)
2. \(x>0, v<0, a<0 \)
3. \(x>0, v<0, a>0 \)
4. \(x>0, v>0, a<0\)
3. Two particles are projected in the air with speed \(v_0\), at angles \(\theta_1\) and \(\theta_2\) to the horizontal, respectively. If the height reached by the first particle is greater than that of the second, then:
| (a) |
the angle of the projection: \(\theta_1>\theta_2\) |
| (b) |
the time of flight: \(T_1>T_2\) |
| (c) |
the horizontal range: \(R_1>R_2\) |
| (d) |
the total energy: \(U_1>U_2\) |
Choose the correct option:
1. (a), (c), (d)
2. (a), (c)
3. (b), (c), (d)
4. (a), (b)
4. The angle between \(\mathrm{A}=\hat{\mathbf{i}}+\hat{\mathbf{j}}\) and \(\mathrm{B}=\hat{\mathbf{i}}-\hat{\mathbf{j}}\) is:
1. \(45^{\circ} \)
2. \(90^{\circ} \)
3. \(-45^{\circ} \)
4. \(180^{\circ}\)
5. A body of mass \(10 ~\text{Kg}\) is acted upon by two perpendicular forces, \(6 ~\text{N}\) and \(8 ~\text{N}.\) The resultant acceleration of the body is:
| (a) |
\(1~\text{ms}^{-2}\) at an angle of \(\text {tan}^{-1} \left(\dfrac{4}{3}\right ) \) w.r.t. \(6 ~\text{N}\) force. |
| (b) |
\(0.2~\text{ms}^{-2}\) at an angle of \(\text {tan}^{-1} \left(\dfrac{3}{4}\right ) \) w.r.t. \(8 ~\text{N}\) force. |
| (c) |
\(1~\text{ms}^{-2}\) at an angle of \(\text {tan}^{-1} \left(\dfrac{3}{4}\right ) \) w.r.t. \(8 ~\text{N}\) force. |
| (d) |
\(0.2~\text{ms}^{-2}\) at an angle of \(\text {tan}^{-1} \left(\dfrac{3}{4}\right ) \) w.r.t. \(6 ~\text{N}\) force. |
Choose the correct option from the given ones:
| 1. |
(a) and (c) |
2. |
(b) and (c) |
| 3. |
(c) and (d) |
4. |
(a), (b) and (c) |
6. A car of mass \(m\) starts from rest and acquires a velocity along the east, \(v=v\mathrm{\hat{i}}(v>0)\) in two seconds. Assuming the car moves with uniform acceleration, the force exerted on the car is:
| 1. |
\(mv/2 \) eastward and is exerted by the car engine. |
| 2. |
\(mv/2\) eastward and is due to the friction on the tires exerted by the road. |
| 3. |
more than \(mv/2\) eastward exerted due to the engine and overcomes the friction of the road. |
| 4. |
\(mv/2\) exerted by the engine. |
7. Two identical ball bearings in contact with each other and resting on a frictionless table is hit head-on by another ball bearing of the same time moving initially with a speed \(v\) as shown in the figure.

If the collision is elastic, which of the following (as depicted in the figure) is a possible result after collision?
8. Which of the diagrams in the figure correctly shows the change in kinetic energy of an iron sphere falling freely in a lake with sufficient density to impart it a terminal velocity?
9. A bicyclist comes to a skidding stop in \(10~\text m.\) During this process, the force on the bicycle due to the road is \(200~\text N\) is directly opposed to the motion. The work done by the cycle on the road is:
1. \(+2000~\text J\)
2. \(-200~\text J\)
3. zero
4. \(-20000~\text J\)
10. A uniform square plate has a small piece \(Q\) of an irregular shape removed and glued to the center of the plate leaving a hole behind in the figure. Then the moment of inertia about the \({z}\text -\)axis is:

| 1. |
increased |
| 2. |
decreased |
| 3. |
the same |
| 4. |
changed in an unpredictable manner |
11. The figure shows a lamina in \(xy\text{-}\)plane. Two axes \({z}\) and \(z'\) pass perpendicular to its plane. A force \(\vec{F}\) acts in the plane of the lamina at point \(P\) as shown in the figure.
(The point \(P\) is closer to the \(z'\text-\)axis than the \(z\text{-}\)axis.)

| (a) |
torque \(\vec{\tau}\)caused by \(\vec{F}\)about \(z\text{-}\)axis is along \((-\hat{k})\) |
| (b) |
torque \(\vec{\tau}'\)caused by \(\vec{F}\)about \(z'\text-\)axis is along \((-\hat{k})\) |
| (c) |
torque caused by \(\vec{F}\)about the \(z\text{-}\)axis is greater in magnitude than that about the \(z'\text-\)axis |
| (d) |
total torque is given by \(\vec{\tau}_{net}=\vec{\tau}+\vec{\tau}'\) |
Choose the correct option from the given ones:
| 1. |
(c) and (d) only |
| 2. |
(a) and (c) only |
| 3. |
(b) and (c) only |
| 4. |
(a) and (b) only |
12. A uniform square plate has a small piece \(Q\) of an irregular shape removed and glued to the center of the plate leaving a hole behind in the figure. The \(COM\) of the plate is now in the following quadrant of the \(x\text-y\) plane.

1. \(\text{I}\)
2. \(\text{II}\)
3. \(\text{III}\)
4. \(\text{IV}\)
13. The following are the given statements:
| (a) |
For a general rotational motion, angular momentum \(L\) and angular velocity \(\omega\) need not to be parallel. |
| (b) |
For a rotational motion about a fixed axis, angular momentum \(L\) and angular velocity \(\omega\) are always parallel. |
| (c) |
For a general translational motion, momentum \(p\) and velocity \(v\) are always parallel. |
| (d) |
For a general translational motion, acceleration \(a\) and velocity \(v\) are always parallel. |
Choose the correct option from the given ones:
| 1. |
(a) and (c) |
2. |
(b) and (c) |
| 3. |
(c) and (d) |
4. |
(a), (b) and (c) |
14. Consider the following statements:
| (a) |
The acceleration due to gravity decreases with increasing altitude. |
| (b) |
The acceleration due to gravity increases with increasing depth (assuming the Earth is of uniform density). |
| (c) |
The acceleration due to gravity increases with increasing latitude. |
| (d) |
The acceleration due to gravity is independent of the Earth's mass. |
Choose the correct option from the given ones:
| 1. |
(b), (d) |
2. |
(a), (c) |
| 3. |
(c), (d) |
4. |
(a), (c), (d) |
15. A copper and a steel wire of the same diameter are connected end to end. A deforming force
\(F\) is applied to this composite wire which causes a total elongation of
\(1\) cm. The two wires will have:
| (a) |
the same stress |
(b) |
different stress |
| (c) |
the same strain |
(d) |
different strain |
Choose the correct option:
| 1. |
(a), (b) |
2. |
(a), (d) |
| 3. |
(b), (c) |
4. |
(c), (d) |
16. For an ideal liquid:
| (a) |
The bulk modulus is infinite. |
| (b) |
The bulk modulus is zero. |
| (c) |
The shear modulus is infinite. |
| (d) |
The shear modulus is zero. |
Choose the correct option from the options given below:
| 1. |
(a) and (d) only |
| 2. |
(b) and (d) only |
| 3. |
(b) and (c) only |
| 4. |
(c) and (d) only |
17. For a surface molecule,
| (a) |
The net force on it is zero. |
| (b) |
There is a net downward force. |
| (c) |
The potential energy is less than that of a molecule inside. |
| (d) |
The potential energy is more than that of a molecule inside. |
Choose the correct alterative/s:
| 1. |
(b), (c) |
2. |
(b), (d) |
| 3. |
(c), (d) |
4. |
(a), (d) |
18. A uniform metallic rod rotates about its perpendicular bisector with constant angular speed. If it is heated uniformly to raise its temperature slightly:
| 1. |
its speed of rotation increases. |
| 2. |
its speed of rotation decreases. |
| 3. |
its speed of rotation remains same. |
| 4. |
its speed increases because its moment of inertia increases. |
19. If an average person jogs, he produces \(14.5 \times10^3\) cal/min. This is removed by the evaporation of sweat. The amount of sweat evaporated per minute (assuming \(1\) kg requires \(580 \times10^3\) cal for evaporation) is:
| 1. |
\(0.25\) kg |
2. |
\(0.50\) kg |
| 3. |
\(0.025\) kg |
4. |
\(0.20\) kg |
20. An ideal gas undergoes an isothermal process from some initial state
\(i\) to the final state
\(𝑓\).
| (a) |
\(dU = 0 \) |
(b) |
\(dQ = 0\) |
| (c) |
\(dQ = dU \) |
(d) |
\(dQ = dW\) |
Choose the correct alternatives:
| 1. |
(a), (b), (c) |
2. |
(a), (d) |
| 3. |
(b), (c), (d) |
4. |
(a), (c), (d) |
21. Diatomic molecules like hydrogen have energies due to both translational as well as rotational motion. The equation in kinetic theory \(PV = \dfrac{2}{3}E,\) \(E\) is:
| 1. |
the total energy per unit volume. |
| 2. |
only the translational part of energy because rotational energy is very small compared to translational energy. |
| 3. |
only the translational part of the energy because during collisions with the wall, pressure relates to change in linear momentum. |
| 4. |
the translational part of the energy because rotational energies of molecules can be of either sign and its average over all the molecules is zero. |
22. A particle is acted simultaneously by mutually perpendicular simple harmonic motion \(x=a \text{cos}𝜔𝑡\) and \(y = a\text{sin} 𝜔 𝑡\). The trajectory of motion of the particle will be:
1. an ellipse
2. a parabola
3. a circle
4. a straight line
23. The displacement of a particle is represented by the equation \(y= 3 \cos \left(\frac{\pi}{4}-\omega t \right)\). The motion of the particle is:
| 1. |
simple harmonic with period \(\dfrac{2\pi}{\omega}\) |
| 2. |
simple harmonic with period \(\dfrac{\pi}{\omega}\) |
| 3. |
periodic but not simple harmonic |
| 4. |
non-periodic |
24. Water waves produced by a motor boat sailing in water are:
1. neither longitudinal nor transverse.
2. both longitudinal and transverse.
3. only longitudinal.
4. only transverse.
25. Sound waves of wavelength \(\lambda\) travelling in a medium with a speed of \(v\) m/s enter into another medium where its speed is \(2v\) m/s. Wavelength of sound waves in the second medium is:
1. \(\lambda \)
2. \(\dfrac{\lambda}{2} \)
3. \(2 \lambda \)
4. \(4 \lambda\)
26. A point charge \(+q\) is placed at a distance \(d\) from an isolated conducting plane. The field at a point \(P\) on the other side of the plane is:
| 1. |
directed perpendicular to the plane and away from the plane. |
| 2. |
directed perpendicular to the plane but towards the plane. |
| 3. |
directed radially away from the point charge. |
| 4. |
directed radially towards the point charge. |
27. Five charges \(q_1, q_2, q_3, q_4~\text{and}~q_5\) are fixed at their positions as shown in the figure, \(S\) is a Gaussian surface. The Gauss' law is given by \(\int_{S}E\cdot dS= \frac{q}{\varepsilon_0}\). Which of the following statements is correct?

| 1. |
\(E\) on the LHS of the above equation will have contribution from \(q_1, q_5~\text{and}~q_3\) while \(q\) on the RHS will have a contribution from \(q_2~\text{and}~q_4\) only. |
| 2. |
\(E\) on the LHS of the above equation will have a contribution from all charges while \(q\) on the RHS will have a contribution from \(q_2~\text{and}~q_4\) only. |
| 3. |
\(E\) on the LHS of the above equation will have a contribution from all charges while \(q\) on the RHS will have a contribution from \(q_1, q_3~\text{and}~q_5\) only. |
| 4. |
Both \(E\) on the LHS and \(q\) on the RHS will have contributions from \(q_2\) and \(q_4\) only. |
28. In a region of constant potential:
| (a) |
the electric field is uniform. |
| (b) |
the electric field is zero. |
| (c) |
there can be no charge inside the region. |
| (d) |
the electric field shall necessarily change if a charge is placed outside the region. |
Choose the correct option:
| 1. |
(b), (c) |
2. |
(a), (c) |
| 3. |
(b), (d) |
4. |
(c), (d) |
29. A parallel plate capacitor is connected to a battery as shown in the figure. Consider two situations.

| A: |
Key \(K\) is kept closed and plates of capacitors are moved apart using insulating handle. |
| B: |
Key \(K\) is opened and plates of capacitors are moved apart using the insulating handle. |
Then:
| (a) |
In A: \(Q\) remains same but \(C\) changes. |
| (b) |
In B: \(V\) remains same but \(C\) changes. |
| (c) |
In A: \(V\) remains same and hence \(Q\) changes. |
| (d) |
In B: \(Q\) remains same and hence \(V\) changes. |
Choose the correct option(s).
1. (a), (b) only
2. (b), (c) only
3. (a), (c), (d) only
4. (c), (d) only
30. In the circuit shown in the figure initially, key \(K_1\) is closed and key \(K_2\) is open. Then \(K_1\) is opened and \(K_2\) is closed (order is important).
(Take \(Q_1\) and \(Q_2\) as charges on \(C_1\) and \(C_2\) and \(V_1\) and \(V_2\) as voltage respectively.)

Then,
| (a) |
charge on \(C_1\) gets redistributed such that \(V_1 =V_2\) |
| (b) |
charge on \(C_1\) gets redistributed such that \(Q'_1= Q'_2\) |
| (c) |
charge on \(C_1\) gets redistributed such that \(C_1V_1+C_2V_2= C_1E\) |
| (d) |
charge on \(C_1\) gets redistributed such that \(Q'_1+Q'_2=Q\) |
Choose the correct option:
1. (a), (d)
2. (a), (b), (c)
3. (b), (d)
4. (a), (b), (c), (d)
31. Two batteries of emf \(\varepsilon_1\) and \(\varepsilon_2\) \((\varepsilon_2 > \varepsilon_1)\) respectively are connected in parallel as shown in the figure.

| 1. |
The equivalent emf \(\varepsilon_{eq}\) of the two cells is between \(\varepsilon_1\) and \(\varepsilon_2\) i.e, \(\varepsilon_1<\varepsilon_{e q}<\varepsilon_2\) |
| 2. |
The equivalent emf \(\varepsilon_{eq}\) is smaller than \(\varepsilon_1\) |
| 3. |
The \(\varepsilon_{eq}\) is given by \(\varepsilon_{e q}=\varepsilon_1+\varepsilon_2\) always |
| 4. |
\(\varepsilon_{eq}\) is independent of internal resistances \(r_1\) and \(r_2\) |
32. A cubical region of space is filled with some uniform electric and magnetic fields. An electron enters the cube across one of its faces with velocity \(v\) and a positron enters via the opposite face with velocity \(-v\). At this instant,
| (a) |
the electric forces on both the particles cause identical accelerations. |
| (b) |
the magnetic forces on both the particles cause equal accelerations. |
| (c) |
both particles gain or lose energy at the same rate. |
| (d) |
the motion of the centre of mass (CM) is determined by \(\vec{B}\) alone. |
Choose the correct option:
1. (a), (b), (c)
2. (a), (c), (d)
3. (b), (c), (d)
4. (c), (d)
33. Two identical current-carrying coaxial loops carry current
\(I\) in an opposite sense. A simple amperian loop passes through both of them once. Calling the loop as
\(C,\)
| (a) |
\(\oint B\cdot dl= \mp 2\mu_0 I\) |
| (b) |
the value of \(\oint B\cdot dl\) is independent of the sense of \(C\). |
| (c) |
there may be a point on \(C\) where \(B\) and \(dl\) are perpendicular. |
| (d) |
\(B\) vanishes everywhere on \(C\). |
Which of the above statements is correct?
| 1. |
(a) and (b) |
2. |
(a) and (c) |
| 3. |
(b) and (c) |
4. |
(c) and (d) |
34. In a permanent magnet at room temperature
1. magnetic moment of each molecule is zero.
2. the individual molecules have non-zero magnetic moment which are all perfectly aligned.
3. domains are partially aligned.
4. domains are all perfectly aligned.
35. A circular coil expands radially in a region of magnetic field and no electromotive force is produced in the coil. This can be because:
| (a) |
the magnetic field is constant. |
| (b) |
the magnetic field is in the same plane as the circular coil and it may or may not vary. |
| (c) |
the magnetic field has a perpendicular (to the plane of the coil) component whose magnitude is decreasing suitably. |
| (d) |
there is a constant magnetic field in the perpendicular (to the plane of the coil) direction. |
Choose the correct option:
| 1. |
(a), (c) |
2. |
(a), (b), (c) |
| 3. |
(b), (c) |
4. |
(c), (d) |
36. The mutual inductance
\(M_{12}\) of coil
\(1\) with respect to coil
\(2\)
| (a) |
increases when they are brought nearer. |
| (b) |
depends on the current passing through the coils. |
| (c) |
increases when one of them is rotated about an axis. |
| (d) |
is the same as \(M_{21}\) of coil \(2\) with respect to coil \(1\). |
Choose the correct option:
1. (a), (d)
2. (a), (b), (c)
3. (b), (d)
4. (c), (d)
37. An inductor of reactance \(1~\Omega\) and a resistor of \(2~\Omega\) are connected in series to the terminals of a \(6~\text{V}\) (RMS) AC source. The power dissipated in the circuit is:
1. \(8~\text{W}\)
2. \(12~\text{W}\)
3. \(14.4~\text{W}\)
4. \(18~\text{W}\)
38. A linearly polarized electromagnetic wave given as \({E}=E_o \hat{{i}} \cos (k z-\omega \mathrm{t})\) is incident normally on a perfectly reflecting infinite wall at \(z=a\). Assuming that the material of the wall is optically inactive, the reflected wave will be given as
1. \({E}_r=-E_o \hat{{i}} \cos (k z-\omega \mathrm{t}).\)
2. \({E}_r=E_o \hat{{i}} \cos (k z+\omega {t})\).
3. \({E}_r=-E_o \hat{{i}} \cos (k z+\omega {t}) \)
4. \({E}_r=E_o \hat{{i}} \sin (k z-\omega {t}) \)
39. An astronomical refractive telescope has an objective of focal length
\(20~\text{m}\) and an eyepiece of focal length
\(2~\text{cm}\).
| (A) |
The length of the telescope tube is \(20.02~\text{m}\). |
| (B) |
The magnification is \(1000\). |
| (C) |
The image formed is inverted. |
| (D) |
An objective of a larger aperture will increase the brightness and reduce chromatic aberration of the image. |
Choose the correct option from the given ones:
| 1. |
(A) and (D) only |
| 2. |
(A), (B) and (C) only |
| 3. |
(B) and (D) only |
| 4. |
(C) and (D) only |
40. A rectangular block of glass
\(ABCD\) has a refractive index
\(1.6\). A pin is placed midway on the face
\(AB\) (see figure). When observed from the face
\(AD\), the pin shall
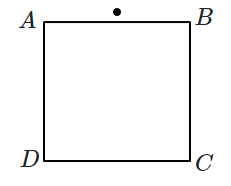
| (a) |
appear to be near \(A\). |
| (b) |
appear to be near \(D\). |
| (c) |
appear to be at the centre of \(AD\). |
| (d) |
not be seen at all. |
Choose the correct option:
| 1. |
(a), (c) |
2. |
(b), (d) |
| 3. |
(c), (d) |
4. |
(a), (d) |
41. Two Sources \(S_1\) and \(S_2 \) of intensity \(I_1\) and \(I_2\) are in front of a screen [Fig.(a)]. The pattern of intensity distribution seen in the central portion is given by Fig.(b).

In this case, which of the following statements are true?
| (a) |
\(S_1\) and \(S_2\) have the same intensities. |
| (b) |
\(S_1\) and \(S_2\) have a constant phase difference. |
| (c) |
\(S_1\) and \(S_2\) have the same phase. |
| (d) |
\(S_1\) and \(S_2\) have the same wavelength. |
Choose the correct option:
| 1. |
(a), (b), (c) |
2. |
(a), (b), (d) |
| 3. |
(b), (c), (d) |
4. |
(c), (d) |
42. For light diverging from a point source:
| (a) |
the wavefront is spherical. |
| (b) |
the intensity decreases in proportion to the distance squared. |
| (c) |
the wavefront is parabolic. |
| (d) |
the intensity at the wavefront does not depend on the distance. |
Choose the correct option:
| 1. |
(a), (b) |
2. |
(a), (c) |
| 3. |
(b), (c) |
4. |
(c), (d) |
43. The wavelength of a photon needed to remove a proton from a nucleus which is bound to the nucleus with \(1~\text{MeV}\) energy is nearly:
1. \(1.2~\text{nm}\)
2. \(1.2\times 10^{-3}~\text{nm}\)
3. \(1.2\times 10^{-6}~\text{nm}\)
4. \(1.2\times 10~\text{nm}\)
44. Consider a beam of electrons (each electron with energy \(E_0\)) incident on a metal surface kept in an evacuated chamber. Then:
| 1. |
no electrons will be emitted as only photons can emit electrons. |
| 2. |
electrons can be emitted but all with energy, \(E_0.\) |
| 3. |
electrons can be emitted with any energy, with a maximum of \({E}_0-\phi\) (\(\phi\) is the work function). |
| 4. |
electrons can be emitted with any energy, with a maximum \(E_0.\) |
45. An ionised \(\text H\)-molecule consists of an electron and two protons. The protons are separated by a small distance of the order of angstrom. In the ground state:
| (a) |
the electron would not move in circular orbits. |
| (b) |
the energy would be \(2^{4}\) times that of a \(\text H\)-atom. |
| (c) |
the electron's orbit would go around the protons. |
| (d) |
the molecule will soon decay in a proton and a \(\text H\)-atom. |
Choose the correct option:
| 1. |
(a), (b) |
2. |
(a), (c) |
| 3. |
(b), (c), (d) |
4. |
(c), (d) |
46. Let \(E_{n} = \frac{- 1m e^{4}}{8 \varepsilon_{0}^{2}n^{2} h^{2}} \) be the energy of the \(n^\text{th}\) level of H-atom. If all the H-atoms are in the ground state and radiation of frequency \(\frac{\left(\right. E_{2} - E_{1} \left.\right)}{h}\) falls on it, then:
| (a) |
it will not be absorbed at all. |
| (b) |
some of the atoms will move to the first excited state. |
| (c) |
all atoms will be excited to the \(n = 2\) state. |
| (d) |
no atoms will make a transition to the \(n = 3\) state. |
Choose the correct option:
| 1. |
(b, d) |
2. |
(a, d) |
| 3. |
(b, c, d) |
4. |
(c, d) |
47. Tritium is an isotope of hydrogen whose nucleus triton contains
\(2\) neutrons and
\(1\) proton. Free neutrons decay into
\(p+e^{-1}+\nu^{-1}.\) If one of the neutrons in Triton decays, it would transform into
\(\mathrm{He}^{3}\) nucleus. This does not happen. This is because:
| 1. |
triton energy is less than that of a \(\mathrm{He}^{3}\) nucleus. |
| 2. |
the electron created in the beta decay process cannot remain in the nucleus. |
| 3. |
both the neutrons in Triton have to decay simultaneously resulting in a nucleus with \(3\) protons, which is not a \(\mathrm{He}^{3}.\) nucleus. |
| 4. |
free neutrons decay due to external perturbations which is absent in the Triton nucleus. |
48. To reduce the ripples in rectifier circuit with capacitor filter:
| (a) |
\(R_L\) should be increased |
| (b) |
input frequency should be decreased |
| (c) |
input frequency should be increased |
| (d) |
capacitors with high capacitance should be used |
Choose the correct option:
| 1. |
(a), (c) |
2. |
(b), (d) |
| 3. |
(a), (c), (d) |
4. |
(b), (c), (d) |
49. The breakdown in a reverse-biased
\(\mathrm{p\text-n}\) junction is more likely to occur due to:
| (a) |
the large velocity of the minority charge carriers if the doping concentration is small. |
| (b) |
the large velocity of the minority charge carriers if the doping concentration is large. |
| (c) |
strong electric field in a depletion region if the doping concentration is small. |
| (d) |
strong electric field in the depletion region if the doping concentration is large. |
Choose the correct option:
1. (a), (d)
2. (b), (d)
3. (c), (d)
4. (b), (c)
50. The conductivity of a semiconductor increases with an increase in temperature,
because:
| 1. |
number density of free current carries increases |
| 2. |
relaxation time increases |
| 3. |
both number density of carries and relaxation time increase |
| 4. |
number density of current carriers increases, relaxation time decreases but the effect of decrease in relaxation time is much less than the increase in number density |
*If above link doesn't work, please go to test link from where you got the pdf and fill OMR from there
CLICK HERE to get FREE ACCESS for 2 days of ANY NEETprep course
















