Physics EXEMPLAR based FST #1

1.

Which of the following measurement is most precise?
1. $5.00~\text{mm}$
2. $5.00~\text{cm}$
3. $5.00~\text{m}$
4. $5.00~\text{km}$

2.

A particle slides down a frictionless parabolic track starting from rest at point $A$. Point $B$ is at the vertex of the parabola and point $C$ is at a height less than that of point $A$. After $C$, the particle moves freely in the air as a projectile. If the particle reaches the highest point at $P$, then,

1.	kinetic energy at $P$ = kinetic energy at $B$
2.	height at $P$ = height at $A$
3.	total energy at $P$ = total energy at $A$
4.	time of travel from $A$ to $B$ = time of travel from $B$ to $P$

3.

Given below in Column-I are the relations between vectors $a,$ $b,$ and $c$ and in Column-II are the orientations of $a,$ $b,$ and $c$ in the $xy$-plane. Match the relation in Column-I to the correct orientations in Column-II.

	Column-I		Column-II
(a)	$a + b = c$	(i)
(b)	$a- c = b$	(ii)
(c)	$b - a = c$	(iii)
(d)	$a + b + c = 0$	(iv)

Choose the correct option from the given table.

1.	a-(ii), b-(iv), c-(iii), d-(i)
2.	a-(i), b-(iii), c-(iv), d-(ii)
3.	a-(iv), b-(iii), c-(i), d-(ii)
4.	a-(iii), b-(iv), c-(i), d-(ii)

4.

For a particle performing uniform circular motion,

(a)	the magnitude of particle velocity (speed) remains constant.
(b)	particle velocity is always perpendicular to the radius vector.
(c)	the direction of acceleration keeps changing as the particle moves.
(d)	angular momentum is constant in magnitude but direction keeps changing.

Choose the correct statement/s:

1.	(c), (d)	2.	(a), (c)
3.	(b), (c)	4.	(a), (b), (c)

5.

A helicopter of mass $2000$ kg rises with a vertical acceleration of $15~\mathrm{m/s^2}$. The total mass of the crew and passengers is $500$ kg. The magnitude of the force on the floor of the helicopter by the crew and passengers is: (Take $g=10~\mathrm{m/s^2}$)
1. $12500~\mathrm{N}$
2. $1250~\mathrm{N}$
3. $50000~\mathrm{N}$
4. $5000~\mathrm{N}$

6. A person of mass $50$ kg stands on a weighing scale on a lift. If the lift is descending with a downward acceleration of $9~\text{ms}^{-2}$, what would be the reading of the weighing scale?
(Take $g=10~\text{ms}^{-2}$)
1. $50~\text{kg}$
2. $5~\text{kg}$
3. $10~\text{kg}$
4. $100~\text{kg}$

7.

Two blocks $M_1$ and $M_2$ having equal mass are free to move on a horizontal frictionless surface. $M_2$ is attached to a massless spring as shown in figure. Initially, $M_2$ is at rest and $M_1$ is moving toward $M_2$ with speed $v $ and collides head-on with $M_2.$

Consider the following given statements:

(a).	while spring is fully compressed, all the kinetic energy of $M_1$ is stored as potential energy of spring.
(b).	while spring is fully compressed, the system's momentum is not conserved, though final momentum is equal to initial momentum.
(c).	if spring is massless, the final state of the $M_1$ is state of rest.
(d).	if the surface on which blocks are moving has friction, then collision cannot be elastic.

Choose the correct option:

1.	only (a)
2.	(a), (b)
3.	(b), (c)
4.	(c), (d)

8.

A body is falling freely under the action of gravity alone in a vacuum. Which of the following quantities remain constant during the fall?

1.	kinetic energy
2.	potential energy
3.	total mechanical energy
4.	total linear momentum

9. In a shotput event, an athlete throws the shotput of mass $10~\text{kg}$ with an initial speed of $1~\text{m/s}$ at $45^\circ$ from a height $1.5~\text{m}$ above ground. Assuming air resistance to be negligible and acceleration due to gravity to be $10~\text{m/s}^2$, the kinetic energy of the shotput when it just reaches the ground will be:
1. $2.5~\text{J}$
2. $5.0~\text{J}$
3. $52.5~\text{J}$
4. $155.0~\text{J}$

10.

A particle of mass $m$ is moving in $yz\text-$plane with a uniform velocity $v$ with its trajectory running parallel to the $+\text{ve}$ $y\text{-}$axis and intersecting $z\text{-}$axis at $z=a$ in the figure. The change in its angular momentum about the origin as it bounces elastically from a wall at $y$ = constant is:

1.	$mva~\hat e_{x}$	2.	$2mva~\hat e_{x}$
3.	$ymva~\hat e_{x}$	4.	$2ymva~\hat e_{x}$

11.

A merry-go-round, made of a ring-like platform of radius $R$ and mass $M,$ is revolving with the angular speed $ω$ . A person of mass $M$ is standing on it. At one instant, the person jumps off the round, radially away from the centre of the round (as seen from the round). The speed of the round afterwards is:
1. $\omega$
2. $2\omega$
3. $\omega/2$
4. $0$

12.

The net external torque on a system of particles about an axis is zero. Which of the following are compatible with it?

(a)	The forces may be acting radially from a point on the axis.
(b)	The forces may be acting on the axis of rotation.
(c)	The forces may be acting parallel to the axis of rotation.
(d)	The torque caused by some forces may be equal and opposite to that caused by other forces.

Choose the correct option.
1. (a, c, d)
2. (a, b, d)
3. (a, b, c, d)
4. (b, c, d)

13.

The density of a non-uniform rod of length 1m is given by $\rho ( x) = a \left( 1 + bx^{2} \right)$ where, $a$, and $b$ are constants and $0 \leq x \leq 1$. The centre of mass of the rod will be at:

1.	$\dfrac{3(2+b)}{4(3+b)}$	2.	$\dfrac{4(2+b)}{3(3+b)}$
3.	$\dfrac{3(3+b)}{4(2+b)}$	4.	$\dfrac{4(3+b)}{3(2+b)}$

14.

Particles of masses $2M, m$ and $M$ are respectively at points $A, B$ and $C$ with $A B = \dfrac{1}{2} \left( B C \right).$ The mass $m$ is much-much smaller than $M$ and at time $t = 0$, they are all at rest as given in the figure. At subsequent times before any collision takes place,

1. $m$ will remain at rest.
2. $m$ will move towards $M.$
3. $m$ will move towards $2M.$
4. $m$ will have oscillatory motion.

15.

A spring is stretched by applying a load to its free end. The strain produced in the spring is:

1. volumetric
2. shear
3. longitudinal and shear
4. longitudinal

16.

A tall cylinder is filled with viscous oil. A round pebble is dropped from the top with zero initial velocity. The plot shown in the figure indicates the one that represents the velocity $(v)$ of the pebble as a function of time $(t).$

1.		2.
3.		4.

17.

An ideal fluid flows through a pipe of circular cross-section made of two sections with diameters $2.5$ cm and $3.75$ cm. The ratio of the velocities in the two pipes is:
1. $9:4$
2. $3:2$
3. $\sqrt{3}:\sqrt{2}$
4. $\sqrt{2}:\sqrt{3}$

18. Three copper blocks of masses $M_{1} , M_{2} $ and $M_{3}~\text{kg}$ respectively are brought into thermal contact till they reach equilibrium. Before contact, they were at $T_{1} , T_{2} , T_{3} \left(\right. T_{1} > T_{2} > T_{3} \left.\right).$ Assuming there is no heat loss to the surroundings, the equilibrium temperature $T$ is:
($s$ is the specific heat of copper)

1.	$T = \dfrac{T_{1} + T_{2} + T_{3}}{3}$
2.	$T = \dfrac{M_{1} T_{1} + M_{2} T_{2} + M_{3} T_{3}}{M_{1} + M_{2} + M_{3}}$
3.	$T = \dfrac{M_{1} T_{1} + M_{2} T_{2} + M_{3} T_{3}}{3 \left(\right. M_{1} + M_{2} + M_{3} \left.\right)}$
4.	$T = \dfrac{M_{1} T_{1} s + M_{2} T_{2} s + M_{3} T_{3} s}{M_{1} + M_{2} + M_{3}}$

19.

The figure shows the $(P\text-V)$ diagram of an ideal gas undergoing a change of state from $A$ to $B.$ Four different paths $\mathrm{I, II, III}$ and $\mathrm{IV},$ as shown in the figure, may lead to the same change of state.

(a)	The change in internal energy is the same in cases $\mathrm{IV}$ and $\mathrm{III}$ but not in cases $\mathrm{I}$ and $\mathrm{II}.$
(b)	The change in internal energy is the same in all four cases.
(c)	The work done is maximum in case $\mathrm{I}.$
(d)	The work done is minimum in case $\mathrm{II}.$

Which of the following options contains only correct statements?

1.	(b), (c) and (d) only	2.	(a) and (d) only
3.	(b) and (c) only	4.	(a), (c) and (d) only

20. In a diatomic molecule, the rotational energy at a given temperature:

(a)	obeys Maxwell’s distribution.
(b)	have the same value for all molecules.
(c)	equals the translational kinetic energy for each molecule.
(d)	is $\frac{2}{3}\text{rd}$ the translational kinetic energy for each molecule.

Choose the correct alternatives:

1.	(a), (b)	2.	(a), (d)
3.	(c), (d)	4.	(a), (c)

21.

The volume versus temperature graphs for a given mass of an ideal gas are shown in the figure at two different values of constant pressure. What can be inferred about relation between $\mathrm{P_1}$ and $\mathrm{P_2}$?

1. $\mathrm{P_1}>\mathrm{P_2} $
2. $\mathrm{P_1}=\mathrm{P_2} $
3. $\mathrm{P_1}<\mathrm{P_2} $
4. data is insufficient

22.

A particle executing SHM has a maximum speed of $30$ cm/s and a maximum acceleration of $60$ cm/s². The period of oscillation is:
1. $\pi $ s
2. $\dfrac{\pi }{2}$ s
3. $2\pi$ s
4. $\dfrac{\pi }{4}$ s

23.

The (displacement-time) graph of a particle executing SHM is shown in the figure. Then:

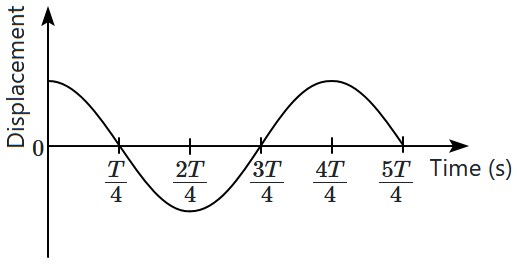
(a)	the force is zero at $t=\dfrac{3T}{4}$
(b)	the acceleration is maximum at $t=\dfrac{4T}{4}$
(c)	the velocity is maximum at $t=\dfrac{T}{4}$
(d)	the potential energy is equal to the kinetic energy of oscillation at $t=\dfrac{T}{2}$

Which of the statement/s given above is/are true?

1.	(a), (b) and (d) only	2.	(a), (b) and (c) only
3.	(b), (c) and (d) only	4.	(c) and (d) only

24.

The displacement of a particle varies with time according to the relation, $y=a~\text{sin} \omega t+b~\text{cos} \omega t.$

1.	the motion is oscillatory but not SHM
2.	the motion is SHM with amplitude $a+b$
3.	the motion is SHM with amplitude $a^{2}+b^{2}$
4.	the motion is SHM with amplitude $\sqrt{a^{2}+b^{2}}$

25.

Boyle's law is applicable for an:

1.	adiabatic process	2.	isothermal process
3.	isobaric process	4.	isochoric process

26.

The electric flux through the surface:

1.	in figure-(iv) is the largest
2.	in figure-(iii) is the least
3.	in figure-(ii) is same as figure-(iii) but is smaller than figure-(iv)
4.	is the same for all the figures

27.

A hemisphere is uniformly charged positively. The electric field at a point on a diameter away from the centre is directed:

1.	perpendicular to the diameter.
2.	parallel to the diameter.
3.	at an angle tilted towards the diameter.
4.	at an angle tilted away from the diameter.

28. Equipotential surfaces:

(a)	are closer in regions of large electric fields compared to regions of lower electric fields.
(b)	will be more crowded near sharp edges of a conductor.
(c)	will be more crowded near regions of large charge densities.
(d)	will always be equally spaced.

Choose the correct option:

1.	(a), (b)	2.	(c), (d)
3.	(a), (b), (c)	4.	(a), (b), (c), (d)

29.

The figure shows some equipotential lines distributed in space. A charged object is moved from point $A$ to point $B$.

Choose the correct option:

1.	The work done in Fig. (i) is the greatest.
2.	The work done in Fig. (ii) is the least.
3.	The work done is the same in Fig. (i), Fig. (ii) and Fig. (iii).
4.	The work done in Fig. (iii) is greater than Fig. (ii) but equal to that in Fig. (i).

30.

Temperature dependence of resistivity $\rho(T)$ of semiconductors, insulators, and metals is significantly based on the following factors:

(a)	number of charge carriers can change with temperature $T$.
(b)	the time interval between two successive collisions can depend on $T$.
(c)	length of material can be a function of $T$.
(d)	mass of carriers is a function of $T$.

Which of the above statements is correct?

1.	(a, b)	2.	(c, d)
3.	(b, c)	4.	(b, d)

31.

The measurement of an unknown resistance $R$ is to be carried out using a Wheatstone bridge. Two students perform an experiment in two ways. The first students take $R_2=10~\Omega$ and $R_1=5~\Omega.$ The other student takes $R_2=1000~\Omega$ and $R_1=500~\Omega.$ In the standard arm, both take $R_3=5~\Omega.$ Both find $R = \dfrac{R_{2}}{R_{1}} \times R_{3} = 10 ~ \Omega $ within errors.

(a)	The errors of measurement of the two students are the same.
(b)	Errors of measurement do depend on the accuracy with which $R_2$ and $R_1$ can be measured.
(c)	If the student uses large values of $R_2$ and $R_1,$ the currents through the arms will be feeble. This will make the determination of the null point accurately more difficult.
(d)	Wheatstone Bridge is a very accurate instrument and has no errors of measurement.

Choose the correct option from the given ones:

1.	(a) and (c) only
2.	(c) and (d) only
3.	(b) and (c) only
4.	(c) and (d) only

32. The gyro-magnetic ratio of an electron in an H-atom, according to the Bohr model, is:

1.	independent of which orbit it is in.
2.	negative.
3.	positive.
4.	increases with the quantum number $n$.

33.

A charged particle would continue to move with a constant velocity in a region wherein,

(A)	$E=0, ~B\ne0$
(B)	$E\ne0, ~B\ne0$
(C)	$E\ne0, ~B=0$
(D)	$E=0, ~B=0$

Choose the correct option:
1. (A), (C)
2. (B), (D)
3. (B), (C), (D)
4. (C), (D)

34. A current-carrying circular loop of radius R is placed in the x-y plane with center at the origin. Half of the loop with x > 0 is now bent so that it now lies in the y-z plane.

1.	The magnitude of the magnetic moment now diminishes.
2.	The magnetic moment does not change.
3.	The magnitude of B at (0, 0, z), z >>R increases.
4.	The magnitude of B at (0, 0, z), z >>R is unchanged.

35. A square of side $L$ meters lies in the $x\text-y$ plane in a region, where the magnetic field is given by ${B}=B_0(2 \hat{i}+3 \hat{j}+4 \hat{k}) ~\text{T}$, where $B_0$ is constant. The magnitude of flux passing through the square is:

1.	$2 B_0 L^2 ~\text{Wb}.$	2.	$3 B_0 L^2 ~\text{Wb}.$
3.	$4 B_0 L^2 ~\text{Wb}.$	4.	$\sqrt{29} B_0 L^2 ~\text{Wb}.$

36.

To reduce the resonant frequency in an LCR series circuit with a generator:

1.	the generator frequency should be reduced
2.	another capacitor should be added in parallel to the first
3.	the iron core of the inductor should be removed
4.	the dielectric in the capacitor should be removed

37.

Which of the following combinations should be selected for better tuning of an LCR circuit used for communication?
1. $R = 20~\Omega,~L= 1.5~\text{H}, ~C = 35~\mu \text{F}$
2. $R = 25~\Omega,~L= 2.5~\text{H}, ~C = 45~\mu \text{F}$
3. $R = 15~\Omega,~L= 3.5~\text{H}, ~C = 30~\mu \text{F}$
4. $R = 25~\Omega,~L= 1.5~\text{H}, ~C = 45~\mu \text{F}$

38.

An EM wave of intensity $I$ falls on a surface kept in a vacuum and exerts radiation pressure $P$ on it. Which of the following are true?

(a)	Radiation pressure is $\frac{I}{c}$ if the wave is totally absorbed.
(b)	Radiation pressure is $\frac{I}{c}$ if the wave is totally reflected.
(c)	Radiation pressure is $\frac{2I}{c}$ if the wave is totally reflected.
(d)	Radiation pressure is in the range $\frac{I}{c}<P<\frac{2I}{c}$ for real surfaces.

Choose the correct one from the given options:

1.	a, b and c	2.	b, c and d
3.	a, c and d	4.	c and d

39. A short pulse of white light is incident from air to a glass slab at normal incidence. After travelling through the slab, the first colour to emerge is
1. blue.
2. green.
3. violet.
4. red.

40. An object approaches a convergent lens from the left of the lens with a uniform speed $5$ m/s and stops at the focus. The image

1.	moves away from the lens with an uniform speed $5$ m/s.
2.	moves away from the lens with an uniform acceleration.
3.	moves away from the lens with a non-uniform acceleration.
4.	moves towards the lens with a non-uniform acceleration.

41.

Consider a ray of light incident from the air onto a slab of glass (refractive index $n$) of width $d$, at an angle $\theta$. The phase difference between the ray reflected by the top surface of the glass and the bottom surface is:
1. $\frac{4 \pi d}{\lambda}\left(1-\frac{1}{n^2} \sin ^2 \theta\right)^{1 / 2}+\pi$
2. $\frac{4 \pi d}{\lambda}\left(1-\frac{1}{n^2} \sin ^2 \theta\right)^{1 / 2}$
3. $\frac{4 \pi d}{\lambda}\left(1-\frac{1}{n^2} \sin ^2 \theta\right)^{1 / 2}+\frac{\pi}{2}$
4. $\frac{4 \pi d}{\lambda}\left(1-\frac{1}{n^2} \sin ^2 \theta\right)^{1 / 2}+2\pi$

42.

In Young's double-slit experiment, the source is white light. One of the holes is covered by a red filter and another by a blue filter. In this case:

1.	there shall be alternate interference patterns of red and blue.
2.	there shall be an interference pattern for red distinct from that for blue.
3.	there shall be no interference fringes.
4.	there shall be an interference pattern for red mixing with one for blue.

43.

A proton, a neutron, an electron and an $\alpha\text-$particle have the same energy. Then, their de-Broglie wavelengths compare as:
1. $\lambda_p= \lambda_n>\lambda_e>\lambda_\alpha$
2. $\lambda_\alpha <\lambda_p = \lambda_n<\lambda_e$
3. $\lambda_e<\lambda_p=\lambda_n>\lambda_\alpha$
4. $\lambda_e =\lambda_p = \lambda_n=\lambda_\alpha$

44.

The wavelength of a photon needed to remove a proton from a nucleus which is bound to the nucleus with $1~\text{MeV}$ energy is nearly:
1. $1.2~\text{nm}$
2. $1.2\times 10^{-3}~\text{nm}$
3. $1.2\times 10^{-6}~\text{nm}$
4. $1.2\times 10~\text{nm}$

45.

The Bohr model for the spectra of a $H$-atom:

(a)	will not apply to hydrogen in the molecular form.
(b)	will not be applicable as it is for a $He$-atom.
(c)	is valid only at room temperature.
(d)	predicts continuous as well as discrete spectral lines.

Choose the correct option:

1.	(a), (b)	2.	(c), (d)
3.	(b), (c)	4.	(a), (d)

46. The gravitational force between $\text H\text-$atom and another particle of mass $m$ will be given by Newton's law $F=\dfrac{GMm}{r^2},$ where $r$ is in $\text{km}$ and;

1.	$M = m_{\text{proton}}+ m_{\text{electron}}.$
2.	$M = m_{\text{proton}}+ m_{\text{electron}}-\frac{B}{c^2}\left(B= 13.6~\text{eV}\right)$.
3.	$M$ is not related to the mass of the hydrogen atom.
4.	$M = m_{\text{proton}}+ m_{\text{electron}}-\frac{\|V\|}{c^2}(\|V\|=$ magnitude of the potential energy of electron in the $\text H\text-$atom).

47. When a nucleus in an atom undergoes a radioactive decay, the electronic energy levels of the atom:

1.	do not change for any type of radioactivity
2.	change for $\alpha$ and $\beta\text-$radioactivity but not for $\gamma\text-$radioactivity
3.	change for $\alpha\text-$radioactivity but not for others
4.	change for $\beta\text-$radioactivity but not for others

48.

In the circuit shown in the figure given below, if the diode forward voltage drop is $0.3~\text V,$ the voltage difference between $A$ and $B$ is:

1.	$1.3~\text V$	2.	$2.3~\text V$
3.	$0$	4.	$0.5~\text V$

49.

A truth table for the given circuit is:

1.	$A$	$B$	$E$	2.	$A$	$B$	$E$
	$0$	$0$	$1$		$0$	$0$	$1$
	$0$	$1$	$1$		$0$	$1$	$0$
	$1$	$0$	$1$		$1$	$0$	$0$
	$1$	$1$	$0$		$1$	$1$	$0$

3.	$A$	$B$	$E$	4.	$A$	$B$	$E$
	$0$	$0$	$0$		$0$	$0$	$0$
	$0$	$1$	$1$		$0$	$1$	$1$
	$1$	$0$	$0$		$1$	$0$	$1$
	$1$	$1$	$1$		$1$	$1$	$0$

50.

In the depletion region of a diode:

(a)	there are no mobile charges
(b)	equal number of holes and electrons exist, making the region neutral
(c)	recombination of holes and electrons has taken place
(d)	immobile charged ions exist

Choose the correct option:

1. (a), (b)
2. (a), (b), (d)
3. (c), (d)
4. All options are correct

Fill OMR Sheet*

*If above link doesn't work, please go to test link from where you got the pdf and fill OMR from there

CLICK HERE to get FREE ACCESS for 2 days of ANY NEETprep course

1.	\(A\)	\(B\)	\(E\)	2.	\(A\)	\(B\)	\(E\)
	\(0\)	\(0\)	\(1\)		\(0\)	\(0\)	\(1\)
	\(0\)	\(1\)	\(1\)		\(0\)	\(1\)	\(0\)
	\(1\)	\(0\)	\(1\)		\(1\)	\(0\)	\(0\)
	\(1\)	\(1\)	\(0\)		\(1\)	\(1\)	\(0\)

3.	\(A\)	\(B\)	\(E\)	4.	\(A\)	\(B\)	\(E\)
	\(0\)	\(0\)	\(0\)		\(0\)	\(0\)	\(0\)
	\(0\)	\(1\)	\(1\)		\(0\)	\(1\)	\(1\)
	\(1\)	\(0\)	\(0\)		\(1\)	\(0\)	\(1\)
	\(1\)	\(1\)	\(1\)		\(1\)	\(1\)	\(0\)

1.	kinetic energy at \(P\) = kinetic energy at \(B\)
2.	height at \(P\) = height at \(A\)
3.	total energy at \(P\) = total energy at \(A\)
4.	time of travel from \(A\) to \(B\) = time of travel from \(B\) to \(P\)

	Column-I		Column-II
(a)	\(a + b = c\)	(i)
(b)	\(a- c = b\)	(ii)
(c)	\(b - a = c\)	(iii)
(d)	\(a + b + c = 0\)	(iv)

1.	\(mva~\hat e_{x}\)	2.	\(2mva~\hat e_{x}\)
3.	\(ymva~\hat e_{x}\)	4.	\(2ymva~\hat e_{x}\)

1.	\(\dfrac{3(2+b)}{4(3+b)}\)	2.	\(\dfrac{4(2+b)}{3(3+b)}\)
3.	\(\dfrac{3(3+b)}{4(2+b)}\)	4.	\(\dfrac{4(3+b)}{3(2+b)}\)

1.	\(T = \dfrac{T_{1} + T_{2} + T_{3}}{3}\)
2.	\(T = \dfrac{M_{1} T_{1} + M_{2} T_{2} + M_{3} T_{3}}{M_{1} + M_{2} + M_{3}}\)
3.	\(T = \dfrac{M_{1} T_{1} + M_{2} T_{2} + M_{3} T_{3}}{3 \left(\right. M_{1} + M_{2} + M_{3} \left.\right)}\)
4.	\(T = \dfrac{M_{1} T_{1} s + M_{2} T_{2} s + M_{3} T_{3} s}{M_{1} + M_{2} + M_{3}}\)

(a)	the force is zero at \(t=\dfrac{3T}{4}\)
(b)	the acceleration is maximum at \(t=\dfrac{4T}{4}\)
(c)	the velocity is maximum at \(t=\dfrac{T}{4}\)
(d)	the potential energy is equal to the kinetic energy of oscillation at \(t=\dfrac{T}{2}\)

1.	the motion is oscillatory but not SHM
2.	the motion is SHM with amplitude \(a+b\)
3.	the motion is SHM with amplitude \(a^{2}+b^{2}\)
4.	the motion is SHM with amplitude \(\sqrt{a^{2}+b^{2}}\)

(A)	\(E=0, ~B\ne0\)
(B)	\(E\ne0, ~B\ne0\)
(C)	\(E\ne0, ~B=0\)
(D)	\(E=0, ~B=0\)

1.	\(2 B_0 L^2 ~\text{Wb}.\)	2.	\(3 B_0 L^2 ~\text{Wb}.\)
3.	\(4 B_0 L^2 ~\text{Wb}.\)	4.	\(\sqrt{29} B_0 L^2 ~\text{Wb}.\)

(a)	Radiation pressure is \(\frac{I}{c}\) if the wave is totally absorbed.
(b)	Radiation pressure is \(\frac{I}{c}\) if the wave is totally reflected.
(c)	Radiation pressure is \(\frac{2I}{c}\) if the wave is totally reflected.
(d)	Radiation pressure is in the range \(\frac{I}{c}<P<\frac{2I}{c}\) for real surfaces.

(a)	will not apply to hydrogen in the molecular form.
(b)	will not be applicable as it is for a \(He\)-atom.
(c)	is valid only at room temperature.
(d)	predicts continuous as well as discrete spectral lines.

1.	\(M = m_{\text{proton}}+ m_{\text{electron}}.\)
2.	\(M = m_{\text{proton}}+ m_{\text{electron}}-\frac{B}{c^2}\left(B= 13.6~\text{eV}\right)\).
3.	\(M\) is not related to the mass of the hydrogen atom.
4.	\(M = m_{\text{proton}}+ m_{\text{electron}}-\frac{\|V\|}{c^2}(\|V\|=\) magnitude of the potential energy of electron in the \(\text H\text-\)atom).

1.	do not change for any type of radioactivity
2.	change for \(\alpha\) and \(\beta\text-\)radioactivity but not for \(\gamma\text-\)radioactivity
3.	change for \(\alpha\text-\)radioactivity but not for others
4.	change for \(\beta\text-\)radioactivity but not for others

Please be patient as the PDF generation may take up to a minute.

Fill OMR Sheet*