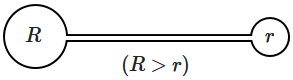1. The energy needed in breaking of a drop of liquid of radius R into n drops of radius r is given by (T is surface tension and P is atmospheric pressure) :
1.
2.
3.
4.
2. The radius of a soap bubble is increased from R to 2R. Work done in this process in terms of surface tension is
1.
2.
3.
4.
3. If the capillary experiment is performed in a vacuum, then for a liquid there capillary rise
(1) It will rise
(2) Will remain the same
(3) It will fall
(4) Rise to the top
4. In a surface tension experiment with a capillary tube, water rises upto 0.1 m. If the same experiment is repeated on an artificial satellite, which is revolving around the earth, water will rise in the capillary tube upto a height of-
(1) 0.1 m
(2) 0.2 m
(3) 0.98 m
(4) Full length of the capillary tube
5. A capillary tube is immersed vertically in the water and the height of the water column is x. When this arrangement is taken into a mine of depth d, the height of the water column is y. If R is the radius of the earth, the ratio x/y is :
1.
2.
3.
4.
6. A mercury drop does not spread on a glass plate because the angle of contact between glass and mercury is:
1. acute
2. obtuse
3. zero
4. \(90^\circ\)
7. The surface tension of a liquid is 10 N/m. If a thin film of liquid is developed in a ring of wire of radius 0.1 m, then surface energy of liquid film will be-
1. 0.314 J
2. 0.48 J
3. 0.56 J
4. 0.63 J
8. The work done to break a spherical drop of radius R into n drops of equal size is equal to:
1.
2.
3.
4.
9. If \(M\) is the mass of water that rises in a capillary tube of radius \(r,\) then mass of water which will rise in a capillary tube of radius \(2r\) is:
1. \(M\)
2. \(4M\)
3. \(M/2\)
4. \(2M\)
10. The ratio of surface tensions of mercury and water is given to be \(7.5:1\) while the ratio of their densities is \(13.6:1\) Their contact angles, with glass, are close to \(135^\circ\) and \(0^\circ,\) respectively. It is observed that mercury gets depressed by an amount \(h\) in a capillary tube of radius \(r_1,\) while water rises by the same amount \(h\) in a capillary tube of radius \(r_2.\) The ratio \(\frac{r_1}{r_2},\) is then close to:
| 1. |
\(\dfrac{2}{3}\) |
2. |
\(\dfrac{4}{5}\) |
| 3. |
\(\dfrac{2}{5}\) |
4. |
\(\dfrac{3}{5}\) |
11. A \(20\) cm-long capillary tube is dipped in water, causing the water to rise to a height of \(8\) cm within the tube. If this setup is then placed inside an elevator that is in free fall, what will be the new height of the water column in the capillary tube?
| 1. |
\(8\) cm |
2. |
\(10\) cm |
| 3. |
\(4\) cm |
4. |
\(20\) cm |
12. Which of the following graphs may represent the relation between the capillary rise \(h\) and the radius \(r\) of the capillary?

1. \(d\)
2. \(b\)
3. \(c\)
4. \(a\)
13. The height to which a liquid rises in a capillary tube depends on:
| (A) |
The material of the tube. |
| (B) |
The length of the tube. |
| (C) |
The outer radius of the tube. |
| (D) |
The inner radius of the tube. |
Choose the correct option from the options given below:
| 1. |
(A) and (B) only |
| 2. |
(A), (B) and (C) only |
| 3. |
(A), (B) and (D) only |
| 4. |
All of the above |
14. The contact angle between a solid and a liquid is a property of:
| (a) |
the material of the solid |
| (b) |
the material of the liquid |
| (c) |
the shape of the solid |
| (d) |
the mass of the solid |
Choose the correct option from the given ones:
1. (a) and (b) only
2. (b) and (c) only
3. (c) and (d) only
4. All of these
15. Choose the incorrect statement:
| 1. |
Soap bubbles have two air-liquid interfaces. |
| 2. |
Liquid drops have one air-liquid interface. |
| 3. |
Air cavity inside a liquid has one air-liquid interface. |
| 4. |
Air cavity inside a liquid has two air-liquid interfaces. |
16. Water rises to a height \(h\) in a capillary tube with a total height of \(2h.\) If the capillary setup is released to fall freely under gravity, what will be the new height of the water in the capillary?
1. \(2h\)
2. \(h\)
3. zero
4. water will spill out
17. Consider a soap film on a square frame of wire of area
\((5\times 5)~\text{cm}^2.\) If the area of the soap film is increased to
\((6\times 6)~\text{cm}^2.\) The work done in the process will be:
(The surface tension of the soap film is
\(4 \times 10^{-2}~\text{N-m}^{-1})\)
| 1. |
\(22\times 10^{-6}~\text J\) |
2. |
\(44\times 10^{-6}~\text J\) |
| 3. |
\(88\times 10^{-6}~\text J\) |
4. |
\(172\times 10^{-6}~\text J\) |
18. Which one of the following cannot be explained on the basis of Bernoulli's theorem?
1. Blowing off of light roofs when strong winds blow.
2. Curved path followed by a spinning ball
3. Working of an atomizer
4. Rise of liquid through a capillary
19. Liquid drops are falling slowly one by one from a vertical glass tube. Establish a relation between the weight \(W\) of a drop, the surface tension \(T,\) and the radius \(r\) of the tube: \(\left({\mathit{\theta}{=}\mathop {0}\nolimits^{\circ}}\right)\)
1. \(W=\pi r^{2}T\)
2. \(W=2\pi rT\)
3. \(W=2\pi r^{2}T \)
4. \(W=\frac{4}{3}(\pi r^{3}T)\)
20. A
\(\text{U}\text-\)tube with limbs of diameters
\(5~\text{mm}\) and
\(2~\text{mm}\) contains water of surface tension
\({7}\times{10}^{{-}{2}}~\text{N/m}\), angle of contact
\(0^{\circ}\) and density
\(10^{3}~\text{kg/m}^3\). If
\(g\) is
\(10~\text{m/s}^2\), then the difference in levels in the two limbs is: (Given: Initially water level in both the limbs is the same and in metres)
| 1. |
\(8.4~\text{mm}\) |
2. |
\(8.4~\text{cm}\) |
| 3. |
\(8.4~\text{m}\) |
4. |
\(0.84~\text{mm}\) |
21. The surface tension of the soap solution is \(0.03~\text{N/m}.\) The work done in blowing to form a soap bubble of surface area \(40~\text{cm}^{2}\) is:
1. \(1.2\times{10}^{-4}~\text{J}\)
2. \(2.4\times{10}^{-4}~\text{J}\)
3. \(12\times 10^{-4}~\text{J}\)
4. \(24\times 10^{-4}~\text{J}\)
22. A small thin tube is connected to two soap bubbles, one of radius
\(R\) and the other radius
\(r\) — so that the air in the two bubbles can flow through the tube. Then, air will flow:
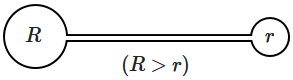
| 1. |
from the larger bubble to the smaller bubble, until the two are of equal size. |
| 2. |
from the large bubble to the smaller bubble initially, and the smaller one becomes larger; then the flow is reversed. |
| 3. |
from the smaller bubble to the larger one until the smaller bubble becomes very small. |
| 4. |
from the larger to the smaller bubble and it bursts the smaller bubble. |
23. Given below are two statements:
| Assertion (A): |
A small drop of mercury is spherical but bigger drops are oval in shape. |
| Reason (R): |
Surface tension of liquid decreases with increase in temperature. |
| 1. |
Both (A) and (R) are True and (R) is the correct explanation of (A). |
| 2. |
Both (A) and (R) are True but (R) is not the correct explanation of (A). |
| 3. |
(A) is True but (R) is False. |
| 4. |
(A) is False but (R) is True. |
24. Given
below are two statements:
| Assertion (A): |
When two soap bubbles of different radii are brought into contact, the common interface of contact bulges into the bubble of larger radii. |
| Reason (R): |
Pressure inside a soap bubble of a lesser radius is more than pressure inside the soap bubble of a larger radius. |
| 1. |
Both (A) and (R) are true and (R) is the correct explanation of (A). |
| 2. |
Both (A) and (R) are true but (R) is not the correct explanation of (A). |
| 3. |
(A) is true but (R) is false. |
| 4. |
Both (A) and (R) are false. |
25. Given below are two statements:
| Assertion (A): |
At the critical temperature, the surface tension of a liquid becomes zero. |
| Reason (R): |
At this temperature, intermolecular forces for liquids and gases become equal. Liquid can expand without any restriction. |
| 1. |
Both (A) and (R) are true and (R) is the correct explanation of (A). |
| 2. |
Both (A) and (R) are true but (R) is not the correct explanation of (A). |
| 3. |
(A) is true but (R) is false. |
| 4. |
Both (A) and (R) are false. |
26. Given below are two statements:
| Assertion (A): |
When a drop breaks apart into smaller drops, the temperature of the drop decreases. |
| Reason (R): |
The surface energy of the drop increases at the cost of internal energy. |
| 1. |
Both (A) and (R) are true and (R) is the correct explanation of (A). |
| 2. |
Both (A) and (R) are true but (R) is not the correct explanation of (A). |
| 3. |
(A) is true but (R) is false. |
| 4. |
Both (A) and (R) are false. |
27. The spherical shape of raindrop is due to:
| 1. |
the density of the liquid |
2. |
the surface tension |
| 3. |
the atmospheric pressure |
4. |
gravity |
28. The angles of contact between the capillary tubes and three liquids in three containers
\(A\),
\(B\), and
\(C\) are
\(30^\circ,\) \(90^\circ\) and
\(120^\circ\) respectively. The level of liquid inside the capillary tubes in containers:
| 1. |
falls in \(B\) and rises in \(C\) |
| 2. |
rises in \(A\) and neither rises nor falls in \(B\) |
| 3. |
falls in \(C\) and rises in \(B\) |
| 4. |
falls in \(A\) and neither rises nor falls in \(B\) |
29. A soup bubble of radius
\(r\) is blown up to form a bubble of radius
\(2r.\) If
\(\sigma\) is the surface tension of soap solution, the energy spent in doing so is: (Assuming surface tension is constant.)
| 1. |
\(3\pi \sigma r^2\) |
2. |
\(6\pi \sigma r^2\) |
| 3. |
\(12\pi \sigma r^2\) |
4. |
\(24\pi \sigma r^2\) |
30. A big drop is divided into \(1000\) identical droplets. If the big drop had surface energy \(U_{i}\) and all small droplets together had a surface energy \(U_{f},\) then \(\dfrac {U_i}{U_f}\) is equal to:
1. \(1/100\)
2. \(10\)
3. \(1/10\)
4. \(1000\)
*If above link doesn't work, please go to test link from where you got the pdf and fill OMR from there
CLICK HERE to get FREE ACCESS for 2 days of ANY NEETprep course