A sample of 0.1 g of water at 100 and normal pressure requires 54 cal of heat energy to convert to steam at 100 . If the volume of the steam produced is 167.1 cc, the change in internal energy of the sample, is
1. 104.3 J
2. 208.7 J
3. 84.5 J
4. 42.2 J
The volume (V) of a monoatomic gas varies with its temperature (T), as shown in the graph. The ratio of work one by the gas, to the heat absorbed by it, when it undergoes a change from state A to state B, is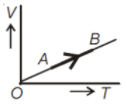
1.
2.
3.
4.
The efficiency of an ideal heat engine working between the freezing point and boiling point of water is
1. 26.8%
2. 20%
3. 12.5%
4. 6.25%
A Carnot engine having an efficiency of as heat engine is used as a refrigerator. If the work done on the system is 10 J, the amount of energy absorbed from the reservoir at a lower temperature is
1. 1 J
2. 90 J
3. 99 J
4. 100 J
Thermodynamic processes are indicated in the following diagram.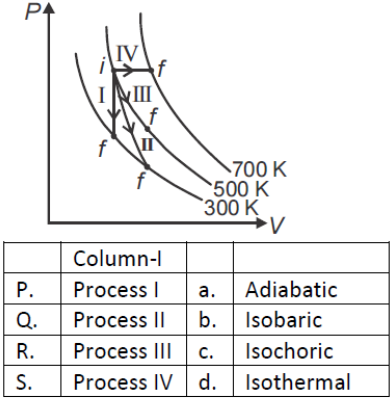
1. P → a, Q → c, R → d, S → b
2. P → c, Q → a, R → d, S → b
3. P → c, Q → d, R → b, S → a
4. P → d, Q → b, R → a, S → C
One mole of an ideal monatomic gas undergoes a process described by the equation = constant. The heat capacity of the gas during this process is
1.
2.
3. 2R
4. R
The temperature inside a refrigerator is °C and the room temperature is °C. The amount of heat delivered to the room for each joule of electrical energy consumed ideally will be
1.
2.
3.
4.
A refrigerator works between and . It is required to remove 600 calories of heat every second in order to keep the temperature of the refrigerated space constant. The power required us [Take 1 cal = 4.2 J)
1. 2365 W
2. 2.365 W
3. 23.65 W
4. 236.5 W
A gas is compressed isothermally to half its initial volume. The same gas is compressed separately through an adiabatic process until its volume is again reduced to half. Then
1. Which of the case (whether compression through isothermal or through the adiabatic process) requires more work will depend upon the automaticity of the gas
2. Compressing the gas isothermally will require more work to be done
3. Compressing the gas through the adiabatic process will require more work to be done
4. Compressing the gas isothermally or adiabatically will require the same amount of work
4.0 g of a gas occupies 22.4 liters at NTP. The specific heat capacity of the gas at constant volume is 5.0 , If the speed of sound in this gas at NTP is 952 , then the heat capacity at constant pressure is (Take gas constant R = 8.3 )
1. 8.5
2. 8.0
3. 7.5
4. 7.0
The coefficient of performance of a refrigerator is 5. If the temperature inside the freezer is , the temperature of the surroundings to which it rejects heat is
1. 20C
2. 31C
3. 41C
4. 11C
An ideal gas is compressed to half its initial volume by means of several processes. Which of the process results in the maximum work done on the gas?
1. Isothermal
2. Adiabatic
3. Isobaric
4. isochoric
One mole of an ideal diatomic gas undergoes a transition from A to B along a path AB as shown in the figure P (in kPa)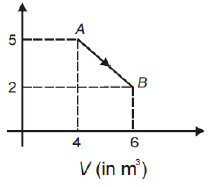
The change in internal energy of the gas during the transition is
1. -12 kJ
2. 20 kJ
3. -20 kJ
4. 20 J
A Carnot engine, having an efficiency of as heat engine, is used as a refrigerator. If the work done on the system is 10 J, the amount of energy absorbed from the reservoir at lower temperature is
1. 1 J
2. 100 J
3. 99 J
4. 90 J
The figure below shows two paths that may be taken by gas to go from a state A to a state C. In process AB, 400 J of heat is added to the system and in-process BC, 100 J of heat is added to the system. The heat absorbed by the system in the process AC will be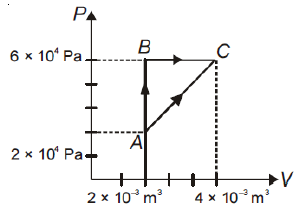
1. 300 J
2. 380 J
3. 500 J
4. 460 J
A monoatomic gas at a pressure P, having a volume V expands isothermally to a volume 2V and then adiabatically to a volume 16V. the final pressure of the gas is : (take y = 5/3)
1. 64P
2. 32P
3. P/64
4. 16P
A thermodynamic system undergoes cyclic process ABCDA as shown in the figure. The work done by the system in the cycle is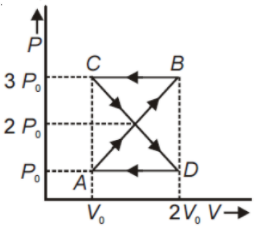
1.
2.
3.
4. Zero
A gas is taken through the cycle ABCA, as shown. What is the network done by the gas?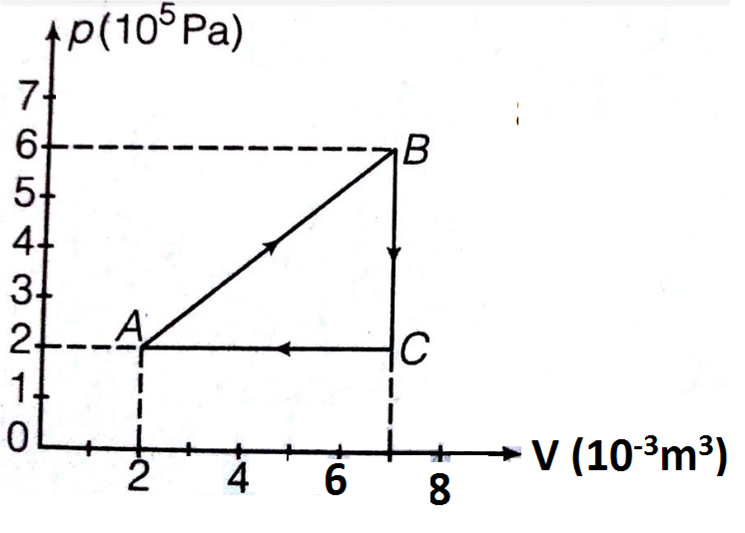
1. 1000 J
2. Zero
3. - 2000 J
4. 2000 J
The molar specific heats of an ideal gas at constant pressure and volume are denoted by respectively. If y = and R is the universal gas constant, then is equal to
1.
2.
3.
4.
During an adiabatic process, the pressure of a gas is foPund to be proportional of a gas is found to be proportional to the cube of its temperature. The ratio of for the gas is :
1. 2
2.
3.
4.
In the given (V-T) diagram, what is the relation between pressures ?
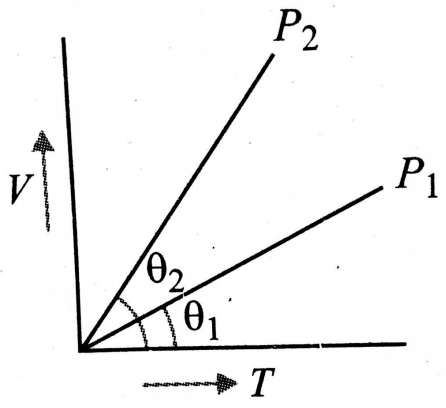
1.
2.
3. Cannot be predicted
4.
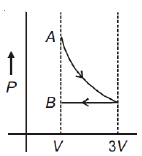
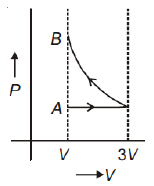
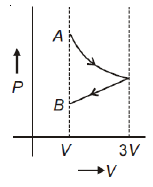
One mole of an ideal gas goes from an initial state A to final state B via two processes: it first undergoes isothermal expansion from volume V to 3V and then its volume is reduced from 3V to V at constant pressure. The correct P-V diagram representing the two processes is
1. 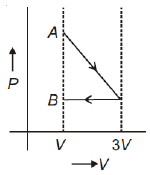
2. 
3. 
4. 
A thermodynamic system is taken through the cycle ABCD as shown in figure. Heat rejected by the gas during the cycle is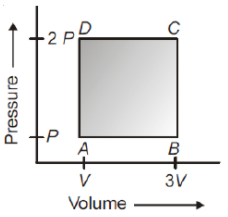
1. PV
2 . PV
3. 2 PV
4. 4 PV
An ideal gas goes from state A to state B via three different processes as indicated in the P-V diagram
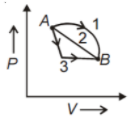
If indicate the heat absorbed by the gas along with the three processes and U1, U2, U3 indicate the change in internal energy along with the three processes respectively, then
1.
2.
3.
4.
During an isothermal expansion, a confined ideal gas does -150 J of work against its surroundings. This implies that
1. 150 J of heat has been added to the gas
2. 150 J oh heart has been removed from the gas
3. 300 J of heart has been added to the gas
4. No heart is transferred because the process is isothermal
A mass of diatomic gas (y = 1.4) at a pressure of 2 atmospheres is compressed adiabatically so that its temperature rised from . The pressure of the gas in the final state is
1. 256 atm
2. 8 atm
3. 28 atm
4. 68.7 atm
If U and W represent the increase in internal energy and work done by the system respectively in a thermodynamical process, which of the following is true? 2010]
1. U = -W, in an isothermal process
2. U = -W, in a adiabatic process
3. U = W, in a isothermal process
4. U = W, in an adiabatic process
If denote the specific heats (per unit mass) of an ideal gas of molecular weight M, where R is the molar gas constant
1.
2.
3.
4.
A monoatomic gas at a pressure is compressed adiabatically to its original volume. What is the final pressure of the gas?
1. 64
2.
3. 16
4. 32
In the thermodynamic process which of the following statements is not true?
1. In an isochoric process, pressure remains constant
2. In an isothermal process, the temperature remains constant
3. In an adiabatic process = constant
4. In an adiabatic process the system is insulated from the surroundings