Please be patient as the PDF generation may take upto a minute.

A stationary observer receives sonic oscillations from two tuning forks, one of which approaches and the other recedes at the same speed. As this takes place the observer hears the beat frequency of 2 Hz. Find the speed of each tuning fork, if their oscillation of frequency is 680 Hz and the velocity if the sound in air is 340 m/s
1.  1 m/s
2.  2 m/s
3.  0.5 m/s
4.  1.5 m/s 

If the equation of a progressive wave is given by $y = 4 \sin \pi \left[\frac{t}{5}-\frac{x}{9}+\frac{\mathrm{\pi }}{6}\right]$ then which of the following is correct?
1.  V = 5 cm/s
2.  $\wedge$ = 18 m
3.  A = 0.04 cm
4.  f = 50 Hz 

The frequency of man's voice is 300 Hz and its wavelength is 1 meter. If the wavelength of a child's voice is  1.5m, then the frequency of the child's voice is
1.  200 Hz
2.  150 Hz
3.  400 Hz
4.  350 Hz 

A string fixed at both ends has consecutive standing wave modes for which the distances between adjacent nodes are 18 cm and 16 cm respectively. The minimum possible length of the string is
1.  144 cm
2.  152 cm
3.  176 cm
4.  200 cm 

The extension in a string, obeying Hooke's law, is x. The speed of a transverse in the stretched string is v. If the extension in the string is increased to 1.5x, the speed of the wave will be
1.  1.22 v
2.  0.61 v
3.  1.50 v
4.  0.75 v 

In the resonance experiment, the first resonance is heard when length of air column is $l_1$ and second resonance is heard when the length of air column is $l_2$. What should be the minimum length of the tube so that third resonance can also be heard
1.  $2l_2 - l_1$
2.  $2l_1$
3.  $5l_1$
4.  $7l_1$

The equation of plane progressive wave motion is $\mathrm{y} = \mathrm{asin}2\mathrm{\pi }/\mathrm{\lambda }\left(\mathrm{vt} - \mathrm{x}\right)$. The velocity of particle is
1. $\mathrm{y}\frac{\mathrm{dv}}{\mathrm{dx}}$
2. $\mathrm{v}\frac{\mathrm{dy}}{\mathrm{dx}}$
3. $\mathrm{y}\frac{\mathrm{dv}}{\mathrm{dx}}$
4. $-\mathrm{v}\frac{\mathrm{dy}}{\mathrm{dx}}$

The third overtone of a closed pipe is observed to be in unison with the second overtone of an open pipe. The ratio of the lengths of the pipes is
1.  3/2
2.  5/3
3.  7/4
4.  7/6

A man standing between two cliffs hears the first echo of a sound after 2 sec and the second echo 3 sec after the initial sound. If the speed of sound is 330 m/s, the distance between the two cliffs should be :
1.  1650 m
2.  990 m
3.  825 m
4.  660 m

Two pulses is a stretch string whose centers are initially 8 cm apart are moving towards each other as shown in the figure. The speed of each pulse is 2 cm/s . After 2 seconds, the total energy of the pulses will be: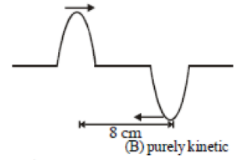

1.  zero
2.  Purely kinetic
3.  Purely potential
4.  Partly kinetic and partly potential 

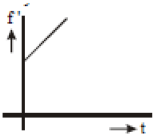
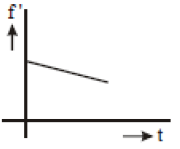
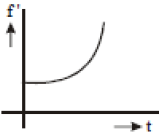
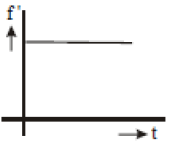
A source of frequency f is stationary and an observer starts moving towards at it t = 0 with constant small acceleration. Then the variation by the observer with time is best represented as 
1.  
2.  
3.  
4.  

The speed of a sound wave in a mixture of 1 mole of helium and 2 moles of oxygen at $27°C$ is
1.  400 m/s
2.  600 m/s
3.  800 m/s
4.  1200 m/s 

A source of the sound of frequency 256 Hz is moving rapidly towards a wall with a velocity of 5 m/sec. If sound travels at a speed of 330 m/sec, then the number of beats per second heard by an observer between the wall and the source is
1.  7.7 Hz
2.  9 Hz
3.  4 Hz
4.  None of these 

If the equation of transverse wave is $- {\mathrm{x}}_0\cos 2\mathrm{\pi }\left(\mathrm{nt} - \frac{\mathrm{x}}{\mathrm{\lambda }}\right)$. Maximum velocity of particle is twice of wave velocity, if $\mathrm{\lambda }$ is
1. $\mathrm{\pi }/2{\mathrm{x}}_0$
2. $2{\mathrm{\pi x}}_0$
3. $\mathrm{\pi x}$
4. ${\mathrm{\pi x}}_0$

Under similar condition of temperature and pressure, in which of the following gases the velocity of sound will be largest
1.  $H_2$
2.  $N_2$
3.  He
4.  $C{O}_2$

Two waves are passing through a region in the same direction at the same time. If the equations of these waves are:
${\mathrm{y}}_1 = \mathrm{asin}\frac{2\mathrm{\pi }}{\mathrm{\lambda }}\left(\mathrm{vt} - \mathrm{x}\right)$ and ${\mathrm{y}}_2 = \mathrm{bsin}\frac{2\mathrm{\pi }}{\mathrm{\lambda }}\left[\left(\mathrm{vt} - \mathrm{x}\right) + {\mathrm{x}}_0\right]$ then the amplitude of the resulting wave for ${\mathrm{x}}_0 = \left(\frac{\mathrm{\lambda }}{2}\right)$ is
1. $\left|\mathrm{a} - \mathrm{b}\right|$
2.  a + b
3. $\sqrt{{\mathrm{a}}^2 + {\mathrm{b}}^2}$
4.  $\sqrt{{\mathrm{a}}^2 + {\mathrm{b}}^2 +\hspace{0.17em}2\mathrm{ab} \cos \mathrm{x}}$

An open pipe is suddenly closed at one end with the result that the frequency of third harmonic of the closed pipe is found to be higher by 100 Hz than the fundamental frequency of the open pipe. The fundamental frequency of the open pipe is 
1.  200 Hz
2.  300 Hz
3.  240 Hz
4.  480 Hz 

When a sound wave is reflected from a wall, the phase difference between the reflected and incident pressure wave is
1.  0
2.  $\pi$
3.  $\pi$/2
4.  $\pi$/4

A wave travels uniformly in all directions from a point source in an isotropic medium. The displacement of the medium at any point distance r from the source may be represented by (A is a constant representing the strength of source) :
1.  $\frac{A}{\sqrt{r}}\sin \left(kr-\omega t\right)$
2.  $A\sqrt{r}\sin \left(kr-\omega t\right)$
3.  $Ar \sin \left(kr-\omega t\right)$
4.  $\sqrt{A} /r \sin \left(kr-\omega t\right)$